第七章 矩阵和向量方法

矩阵是一个由双精度、浮点或复数组成的二维数组。

向量是一个由双精度、浮点或复数组成的一维数组。 向量没有指出它是垂直的还是水平的。 它的判定应来自应用的上下文。 例如，向量运算不会假设左侧向量是水平的，右侧向量是垂直的。 如果需要类型指示，则可以采用一行或一列的矩阵。 然而，这通常没有必要。

矩阵和向量为数据动态分配内存。 事实上，矩阵和向量是具有某些属性的对象，诸如它们包含的数据类型和维度。 矩阵和向量属性可以调用 vector_a.Size()、Matrix_b.Rows()、vector_c.Norm()、matrix_d.Cond() 等方法获取。 任何维度都可以更改。

在创建和初始化矩阵时，采用的是所谓的静态方法（这些方法就像类的静态方法）。 例如: matrix::Eye(), matrix::Identity(), matrix::Ones(), vector::Ones(), matrix: :Zeros(), vector::Zeros(), matrix::Full(), vector::Full(), matrix::Tri()。

此刻，矩阵和向量运算并不意味着运用复杂的数据类型，因为这一发展方向尚未完成。

MQL5 支持将矩阵和向量传递至 DLL。 这样就能够从外部变量导入相关类型的函数。

矩阵和向量以指向缓冲区的指针形式被传递到 DLL。 例如，若要传递浮点类型的矩阵，从 DLL 导出的函数，其相应参数必须采用浮点类型的缓冲区指针。

MQL5

#import "mmlib.dll"
bool sgemm(uint flags, matrix<float> &C, const matrix<float> &A, const matrix<float> &B, ulong M, ulong N, ulong K, float alpha, float beta);
#import

C++

extern "C" __declspec(dllexport) bool sgemm(UINT flags, float *C, const float *A, const float *B, UINT64 M, UINT64 N, UINT64 K, float alpha, float beta)

除了缓冲区之外，还应该传递矩阵和向量的大小，方可进行正确处理。

下面按字母顺序列出了所有矩阵和向量方法。

函数	功能	分类
Activation	计算激活函数值，并将其写入传递的向量/矩阵	机器学习
ArgMax	返回最大值的索引	统计
ArgMin	返回最小值的索引	统计
ArgSort	返回排序后的索引	操纵
Assign	复制矩阵、向量或数组，并自动转换	初始化
Average	计算矩阵/向量值的加权平均值	统计
Cholesky	计算乔列斯基（Cholesky）分解	变换
Clip	将矩阵/向量的元素限定到给定的有效值范围	操纵
Col	返回列向量。 将向量写入指定的列。	操纵
Cols	返回矩阵中的列数	特征
Compare	以指定的精度比较两个矩阵/向量的元素	操纵
CompareByDigits	将两个矩阵/向量的元素按有效数字精度进行比较	操纵
Cond	计算一个矩阵的条件数	特征
Convolve	返回两个向量的离散线性卷积	乘积
Copy	返回给定矩阵/向量的副本	操纵
CopyIndicatorBuffer	将指定数量中指定指标缓冲区的数据获取到向量	初始化
CopyRates	获取指定品种、周期、数量的历史序列，格式为 MqlRates 结构，并存储到矩阵或向量	初始化
CopyTicks	从 MqlTick 结构获取跳价，存储到矩阵或向量中	初始化
CopyTicksRange	从 MqlTick 结构获取跳价，以指定数据范围存储到矩阵或向量中	初始化
CorrCoef	计算皮尔逊（Pearson）相关系数（线性相关系数）	乘积
Correlate	计算两个向量的互相关性	乘积
Cov	计算协方差矩阵	乘积
CumProd	返回矩阵/向量元素的累积乘积，包括沿给定轴的累积乘积	统计
CumSum	返回矩阵/矢量元素的累积总和，包括沿给定轴的矩阵/矢量元素	统计
Derivative	计算激活函数导数值，并将其写入所传递的向量/矩阵	机器学习
Det	计算平方可逆矩阵的行列式	特征
Diag	提取对角线或构造对角矩阵	操纵
Dot	两个向量的点积	乘积
Eig	计算方阵的本征值和右本征向量	变换
EigVals	计算一般矩阵的本征值	变换
Eye	返回一个矩阵，对角线上为 1，其它地方为 0	初始化
Fill	用指定值填充现有矩阵或向量	初始化
Flat	通过一个索引替代两个索引访问矩阵元素	操纵
Full	创建并返回新矩阵，并以给定值填充	初始化
GeMM	GeMM（通用矩阵乘法）方法实现了两个矩阵的一般乘法	乘积
HasNan	返回矩阵/向量中NaN值的数量	操纵
Hsplit	将矩阵水平拆分为多个子矩阵。 与 axis=0 的拆分相同	操纵
Identity	创建指定大小的单位矩阵	初始化
Init	矩阵或向量初始化	初始化
Inner	两个矩阵的内积	乘积
Inv	用乔丹-高斯（Jordan-Gauss）方法计算平方可逆矩阵的乘法逆	解法
Kron	返回两个矩阵、矩阵和向量，向量和矩阵、或两个向量的克罗内克（Kronecker）乘积	乘积
LinearRegression	计算包含计算的线性回归值的向量/矩阵	统计
Loss	计算损失函数值，并将其写入所传递的向量/矩阵	机器学习
LstSq	返回线性代数方程的最小二乘解（对于非二乘或退化矩阵）	解法
LU	实现矩阵的 LU 分解：下三角矩阵和上三角矩阵的乘积	变换
LUP	以部分排列实现 LUP 分解，这仅指具有行排列的 LU 分解：PA=LU	变换
MatMul	两个矩阵的矩阵乘积	乘积
Max	返回矩阵/向量中的最大值	统计
Mean	计算元素值的算术平均值	统计
Median	计算矩阵/向量元素的中位数	统计
Min	返回矩阵/向量中的最小值	统计
Norm	返回矩阵或向量范数	特征
Ones	创建并返回一个新矩阵，其中以 1 填充	初始化
Outer	计算两个矩阵或两个向量的外积	乘积
Percentile	返回矩阵/向量元素，或沿指定轴的元素值的指定百分位数	统计
PInv	遵照摩尔-彭罗斯（Moore-Penrose）方法计算矩阵的伪逆	解法
Power	将方阵提高整数幂	乘积
Prod	返回矩阵/向量元素的乘积，也可以针对给定轴执行	统计
Ptp	返回矩阵/向量或给定矩阵轴的数值范围	统计
QR	计算矩阵的 QR 分解	变换
Quantile	返回矩阵/向量元素，或沿指定轴的元素值的指定分位数	统计
Rank	返回利用高斯（Gaussian）方法的矩阵秩	特征
RegressionMetric	在指定数据数组上构建回归线，并计算回归量程作为偏差误差	统计
Reshape	在不更改矩阵数据的情况下更改矩阵的形状	操纵
Resize	返回形状和大小均已更改的新矩阵	操纵
Row	返回行向量。 将向量写入指定行	操纵
Rows	返回矩阵中的行数	特征
Set	根据指定索引设置向量元素值	操纵
Size	返回向量的大小	特征
SLogDet	计算矩阵行列式的符号和对数	特征
Solve	求解线性矩阵方程或线性代数方程组	解法
Sort	按位置排序	操纵
Spectrum	计算矩阵的谱作为其本征值的集合，来自乘积 AT*A	特征
Split	将矩阵拆分为多个子矩阵	操纵
Std	返回矩阵/向量元素，或沿指定轴的元素值的标准偏差	统计
Sum	返回矩阵/矢量元素的总和，也可以针对给定的轴（多轴）执行	统计
SVD	奇异值分解	变换
SwapCols	交换矩阵中的列	操纵
SwapRows	交换矩阵中的行	操纵
Trace	返回矩阵对角线的总和	特征
Transpose	转置（轴交换）并返回修改后的矩阵	操纵
Tri	构造一个矩阵，在指定的对角线上及以下为 1，在其它地方为零	初始化
TriL	返回矩阵的副本，其中第 k 个对角线以上的元素归零。 下三角矩阵	操纵
TriU	返回矩阵的副本，其中第 k 个对角线下方的元素归零。 上三角矩阵	操纵
Var	计算矩阵/向量元素值的方差	统计
Vsplit	将矩阵垂直拆分为多个子矩阵。 axis=1 的拆分相同	操纵
Zeros	创建并返回一个新矩阵，填充零	初始化

7.1 矩阵和向量类型

矩阵和向量是 MQL5 中支持线性代数运算的特殊数据类型。 存在以下数据类型：

• matrix ― 包含双精度元素的矩阵。
• matrixf ― 包含浮点元素的矩阵。
• matrixc ― 包含复数元素的矩阵。
• vector ― 包含双精度元素的向量。
• vectorf ― 包含浮点元素的向量。
• vectorc ― 包含复数元素的向量。

模板函数支持 matrix<double>、matrix<float>、vector<double>、vector<float> 等表示法，替代相应的类型。

矩阵和向量初始化方法

函数	功能
Eye	返回一个矩阵，对角线上为 1，其它地方为 0
Identity	创建指定大小的单位矩阵
Ones	创建并返回一个新矩阵，其中以 1 填充
Zeros	创建并返回一个新矩阵，填充零
Full	创建并返回新矩阵，并按给定值填充
Tri	构造一个矩阵，其中位于给定对角线为 一，而其它地方为零
Init	初始化矩阵或向量
Fill	用指定值填充现有矩阵或向量

7.2 初始化

有若干种方法可以声明和初始化矩阵和向量。

函数	动作
Assign	复制矩阵、向量或数组，并自动转换
CopyIndicatorBuffer	将指定数量中指定指标缓冲区的数据获取到向量
CopyRates	获取指定品种、周期、数量的历史序列，格式为 MqlRates 结构，并存储到矩阵或向量
CopyTicks	从 MqlTick 结构获取跳价，存储到矩阵或向量中
CopyTicksRange	从 MqlTick 结构获取跳价，以指定数据范围存储到矩阵或向量中
Eye	返回一个矩阵，对角线上为 1，其它地方为 0
Identity	创建指定大小的单位矩阵
Ones	创建并返回一个新矩阵，其中以 1 填充
Zeros	创建并返回一个新矩阵，填充零
Full	创建并返回新矩阵，并按给定值填充
Tri	构造一个矩阵，其中位于给定对角线为 一，而其它地方为零
Init	初始化矩阵或向量
Fill	用指定值填充现有矩阵或向量

声明且未指定大小（没有为数据分配内存）：

  matrix         matrix_a;   // 双精度型矩阵
  matrix<double> matrix_a1;  // 声明双矩阵的另一种途径；可以在模板中使用
  matrixf        matrix_a2;  // 浮点型矩阵
  matrix<float>  matrix_a3;  // 浮点型矩阵
  vector         vector_a;   // 双精度向量
  vector<double> vector_a1;
  vectorf        vector_a2;  // 双精度向量
  vector<float>  vector_a3;

声明且指定大小（为数据分配内存，但未初始化）：

  matrix         matrix_a(128,128);           // 参数既可是常数
  matrix<double> matrix_a1(InpRows,InpCols);  // 亦或变量
  matrixf        matrix_a2(1,128);            // 水平向量的模拟
  matrix<float>  matrix_a3(InpRows,1);        // 垂直向量的模拟
  vector         vector_a(256);
  vector<double> vector_a1(InpSize);
  vectorf        vector_a2(SomeFunc());       // 函数 SomeFunc 返回一个 ulong 型的数字，用于设置向量大小
  vector<float>  vector_a3(InpSize+16);       // 表达式可以用作参数

声明且初始化（矩阵和向量大小由初始化序列确定）：

  matrix         matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix<double> matrix_a1=matrix_a;                      // 必须是相同类型的矩阵
  matrixf        matrix_a2={{1,0,0},{0,1,0},{0,0,1}};
  matrix<float>  matrix_a3={{1,2},{3,4}};
  vector         vector_a={-5,-4,-3,-2,-1,0,1,2,3,4,5};
  vector<double> vector_a1={1,5,2.4,3.3};
  vectorf        vector_a2={0,1,2,3};
  vector<float>  vector_a3=vector_a2;                     // 必须是相同类型的向量

声明且初始化：

template<typename T>
void MatrixArange(matrix<T> &mat,T value=0.0,T step=1.0)
  {
   for(ulong i=0; i<mat.Rows(); i++)
     {
      for(ulong j=0; j<mat.Cols(); j++,value+=step)
         mat[i][j]=value;
     }
  }
template<typename T>
void VectorArange(vector<T> &vec,T value=0.0,T step=1.0)
  {
   for(ulong i=0; i<vec.Size(); i++,value+=step)
      vec[i]=value;
  }
...
 
  matrix  matrix_a(size_m,size_k,MatrixArange,-M_PI,0.1); // 首先创建一个大小 size_m x size_k 的未初始化矩阵，然后调用带有初始化时指定参数的 MatrixArange 函数
  matrixf matrix_a1(10,20,MatrixArange);                  // 创建矩阵后，调用带有默认参数的 MatrixArange 函数
  vector  vector_a(size,VectorArange,-10.0);              // 创建向量后，调用带有一个参数的 VectorArange 函数，而第二个参数采用默认值
  vectorf vector_a1(128,VectorArange);

请注意，矩阵或矢量大小可以更改，因为数据的内存始终是动态的。

静态方法 依据指定大小创建矩阵和向量的静态方法，并以某种方式初始化：

  matrix         matrix_a =matrix::Eye(4,5,1);
  matrix<double> matrix_a1=matrix::Full(3,4,M_PI);
  matrixf        matrix_a2=matrixf::Identity(5,5);
  matrixf<float> matrix_a3=matrixf::Ones(5,5);
  matrix         matrix_a4=matrix::Tri(4,5,-1);
  vector         vector_a =vector::Ones(256);
  vectorf        vector_a1=vector<float>::Zeros(16);
  vector<float>  vector_a2=vectorf::Full(128,float_value);

已创建矩阵和向量的初始化方法：

  matrix  matrix_a;
  matrix_a.Init(size_m,size_k,MatrixArange,-M_PI,0.1);
  matrixf matrix_a1(3,4);
  matrix_a1.Init(10,20,MatrixArange);
  vector  vector_a;
  vector_a.Init(128,VectorArange);
  vectorf vector_a1(10);
  vector_a1.Init(vector_size,VectorArange,start_value,step);
 
  matrix_a.Fill(double_value);
  vector_a1.Fill(FLT_MIN);
  matrix_a1.Identity();

7.2.1 Assign

复制矩阵、向量或数组，且带有自动转换。

bool matrix::Assign(
  const matrix<T>  &mat     // 复制的矩阵
   );
bool matrix::Assign(
  const void       &array[] // 复制的数组
   );
bool vector::Assign(
  const vector<T>  &vec     // 复制的向量
   );
bool vector::Assign(
  const void       &array[] // 复制的数组
   );

参数

m, v 或 array

[输入] 需复制的源矩阵、向量或数组。

返回值

如果成功则返回 true，否则返回 ― false。

注意

不同于 Copy，Assign 方法还允许复制数组。 在这种情况下，将进行自动转换，同时生成的矩阵或向量会根据复制数组的大小进行调整。

示例:

//--- 复制矩阵
  matrix a= {{2, 2}, {3, 3}, {4, 4}};
  matrix b=a+2;
  matrix c;
  Print("matrix a \n", a);
  Print("matrix b \n", b);
  c.Assign(b);
  Print("matrix c \n", a);
 
//--- 复制数组到矩阵
  matrix double_matrix=matrix::Full(2,10,3.14);
  Print("double_matrix before Assign() \n", double_matrix);
  int int_arr[5][5]= {{1, 2}, {3, 4}, {5, 6}};
  Print("int_arr: ");
  ArrayPrint(int_arr);
  double_matrix.Assign(int_arr);
  Print("double_matrix after Assign(int_arr) \n", double_matrix);  
  /*
   matrix a
   [[2,2]
    [3,3]
    [4,4]]
   matrix b
   [[4,4]
    [5,5]
    [6,6]]
   matrix c
   [[2,2]
    [3,3]
    [4,4]]
 
   double_matrix before Assign() 
   [[3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]
    [3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]]
    
   int_arr: 
       [,0][,1][,2][,3][,4]
   [0,]   1   2   0   0   0
   [1,]   3   4   0   0   0
   [2,]   5   6   0   0   0
   [3,]   0   0   0   0   0
   [4,]   0   0   0   0   0
   
   double_matrix after Assign(int_arr) 
   [[1,2,0,0,0]
    [3,4,0,0,0]
    [5,6,0,0,0]
    [0,0,0,0,0]
    [0,0,0,0,0]]
 
  */

相关参考

Copy

7.2.2 CopyIndicatorBuffer

将指定数量中指定指标缓冲区的数据获取到向量。

数据将被复制到向量中，定位到为该向量分配的物理内存开头的最早元素。共有三个函数选项。

根据初始位置和所需元素的数量进行访问

bool  vector::CopyIndicatorBuffer(
   long      indicator_handle,     // 指标句柄
   ulong     buffer_index,         // 指标缓冲区编号
   ulong     start_pos,            // 要复制的开始位置
   ulong     count                 // 要复制的元素数量
   );

根据开始日期和所需元素的数量进行访问

bool  vector::CopyIndicatorBuffer(
   long      indicator_handle,     // 指标句柄
   ulong     buffer_index,         // 指标缓冲区编号
   datetime  start_time,           // 复制的开始日期
   ulong     count                 // 复制的元素数量
   );

根据所需时间间隔的初始日期和最终日期进行访问

bool  vector::CopyIndicatorBuffer(
   long      indicator_handle,     // 指标句柄
   ulong     buffer_index,         // 指标缓冲区编号
   datetime  start_time,           // 复制的开始日期
   datetime  stop_time             // 复制的结束日期
   );

参数

indicator_handle

[in] 由相关指标函数获得的指标句柄。

buffer_index

[in] 指标缓存区的编号。

start_pos

[in] 第一个复制元素的索引编号。

count

[in] 复制的元素数。

start_time

[in] 第一个元素对应的柱形图时间。

stop_time

[in] 最后一个元素对应的柱形图时间。

返回值

如果成功，函数返回'true'，如果出现错误则返回'false'。

注意

复制数据的元素（索引为buffer_index的指标缓冲区）从现在到过去进行计数，因此起始位置等于0表示当前柱形图（当前柱形图的指标值）。

当复制未知数量的数据时，您应该声明一个不指定大小的向量（不为数据分配内存），因为CopyBuffer()函数试图将接收向量的大小分配给复制数据的大小。

当需要部分复制指标值时，应该使用一个中间向量，将所需的数量复制到其中。从这个中间向量，您可以逐个成员地将所需数量的值复制到接收向量的所需位置

如果要复制预定数量的数据，建议预先声明一个向量并指定其大小，以避免不必要的内存重新分配。

从指标请求数据时，如果请求的时间序列尚未构建或需要从服务器下载，则该函数立即返回false，同时启动加载/构建。

当从EA或脚本请求数据时，如果程序端在本地没有合适的数据，则启动从服务器下载，或者如果可以从本地历史构建数据，但所需的时间序列尚未准备好，则开始构建必要的时间序列。该函数返回在超时到期时将准备好的数量。

另见

CopyBuffer

7.2.3 CopyRates

获取 MqlRates 结构的历史序列，按指定品种-周期，按指定数量，并存储到矩阵或向量当中。 元素顺序倒计时，从现在到过去，这意味着起始位置等于 0 表示当前柱线。

复制数据，以便将最久远的元素放置在矩阵/向量的开头。 有三个函数选项。

依据初始位置和所需元素的数量进行访问

bool  CopyRates(
   string           symbol,       // 品名
   ENUM_TIMEFRAMES  period,       // 周期
   ulong            rates_mask,   // 指定所请求序列的标志组合
   ulong            start,        // 复制初始柱线的起始索引
   ulong            count         // 要复制的数量
   );

按初始日期和所需元素的数量进行访问

bool  CopyRates(
   string           symbol,       // 品名
   ENUM_TIMEFRAMES  period,       // 周期
   ulong            rates_mask,   // 指定所请求序列的标志组合
   datetime         from,         // 起始日期
   ulong            count         // 要复制的数量
   );

按所需时间间隔的初始日期和最终日期进行访问

bool  CopyRates(
   string           symbol,       // 品名
   ENUM_TIMEFRAMES  period,       // 周期
   ulong            rates_mask,   // 指定所请求序列的标志组合
   datetime         from,         // 起始日期
   datetime         to            // 结束日期
   );

参数

symbol

[输入] 品种。

period

[输入] 周期。

rates_mask

[输入] 指定所请求序列类型的标志的 ENUM_COPY_RATES 枚举组合。 当复制到向量时，只能指定来自 ENUM_COPY_RATES 枚举中的一个值，否则会发生错误。

start

[输入] 第一个复制的元素索引。

count

[输入] 复制的元素数量。

from

[输入] 对应于第一个元素的柱线时间。

to

[输入] 对应于最后一个元素的柱线时间。

返回值

如果成功则返回 true，否则返回 false（如果出现错误）。

注意

如果所请求数据的区间完全超出服务器上的可用数据，则该函数返回 false。 如果数据超出 TERMINAL_MAXBARS 之外（图表上的最大柱数），则该函数也会返回 false。

当请求数据来自 EA 或脚本时，如果终端在本地没有相应的数据，则启动从服务器下载，或者如果可以从本地历史构建数据但尚未准备好，则开始构建必要的时间序列。 该函数按时间返回准备好的直至期满的数据量，然而历史记录下载将继续，并且在下一个类似请求期间，该函数会返回更多数据。

按开始日期和所需项目数量请求数据时，仅返回日期小于（之前）或等于指定日期的数据。 设置间隔时要考虑多一秒。 换句话说，返回值的任何柱线的开盘日期（交易量、点差、开盘价、最高价、最低价、收盘价或时间）始终等于或小于指定的日期。

当请求给定日期范围内的数据时，仅返回请求间隔内的数据。 设置间隔时要考虑多一秒。 换句话说，返回的任何柱线的开盘时间（交易量、点差、指标缓冲区值、开盘价、最高价、最低价、收盘价或时间）始终位于请求的区间内。

例如，如果当日是一周中的星期六，则当尝试设置 start_time=Last_Tuesday 和 stop_time=Last_Friday 复制周线时间帧数据时，函数会返回 0，因为周线时间帧的开盘时间始终落在星期日，故没有一个周线柱线落在指定范围内。

如果您需要获取对应于当前未完成柱线的数值，那么您可以采用第一种调用形式指示 start_pos=0 和 count=1。

ENUM_COPY_RATES

ENUM_COPY_RATES 枚举包含指定要传递给矩阵或数组的数据类型的标志。 标志组合允许在一个请求中从历史记录中获取多个序列。 矩阵中行的顺序将与 ENUM_COPY_RATES 枚举中值的顺序相对应。 换言之，含有最高价数据的行在矩阵中将始终高于含有最低价数据的行。

ID	值	说明
COPY_RATES_OPEN	1	开盘价序列
COPY_RATES_HIGH	2	最高价序列
COPY_RATES_LOW	4	最低价序列
COPY_RATES_CLOSE	8	收盘价序列
COPY_RATES_TIME	16	时间序列（柱线开盘时间）
COPY_RATES_VOLUME_TICK	32	跳价的成交量
COPY_RATES_VOLUME_REAL	64	交易成交量
COPY_RATES_SPREAD	128	点差
组合
COPY_RATES_OHLC	15	开盘价、最高价、最低价、和收盘价序列
COPY_RATES_OHLCT	31	开盘价、最高价、最低价、收盘价、和时间序列
数据排列
COPY_RATES_VERTICAL	32768	序列沿垂直轴复制到矩阵中。接收到的序列值将在矩阵中垂直排列，即最早的数据将位于第一行，而最新的数据将位于矩阵的最后一行。

示例:

//+------------------------------------------------------------------+
//| 脚本程序 start 函数                                                |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- 获取报价至矩阵
  matrix matrix_rates;
  if(matrix_rates.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_OHLCT, 1, 10))
    Print("matrix rates: \n", matrix_rates);
  else
    Print("matrix_rates.CopyRates failed. Error ", GetLastError());
//--- 检查
  MqlRates mql_rates[];
  if(CopyRates(Symbol(), PERIOD_CURRENT, 1, 10, mql_rates)>0)
   {
    Print("mql_rates array:");
    ArrayPrint(mql_rates);
   }
  else
    Print("CopyRates(Symbol(), PERIOD_CURRENT,1, 10, mql_rates). Error ", GetLastError());
//--- 获取报价至向量 = 无效调用
  vector vector_rates;
  if(vector_rates.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_OHLC, 1, 15))
    Print("vector_rates COPY_RATES_OHLC: \n", vector_rates);
  else
    Print("vector_rates.CopyRates COPY_RATES_OHLC failed. Error ", GetLastError());
//--- 获取收盘价至向量
  if(vector_rates.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_CLOSE, 1, 15))
    Print("vector_rates COPY_RATES_CLOSE: \n", vector_rates);
  else
    Print("vector_rates.CopyRates failed. Error ", GetLastError());
 };
/*
   matrix rates:
   [[0.99686,0.99638,0.99588,0.99441,0.99464,0.99594,0.99698,0.99758,0.99581,0.9952800000000001]
    [0.99708,0.99643,0.99591,0.9955000000000001,0.99652,0.99795,0.99865,0.99764,0.99604,0.9957]
    [0.9961100000000001,0.99491,0.99426,0.99441,0.99448,0.99494,0.9964499999999999,0.99472,0.9936,0.9922]
    [0.99641,0.99588,0.99441,0.99464,0.99594,0.99697,0.99758,0.99581,0.9952800000000001,0.99259]
    [1662436800,1662440400,1662444000,1662447600,1662451200,1662454800,1662458400,1662462000,1662465600,1662469200]]
   mql_rates array:
                    [time]  [open]  [high]   [low] [close] [tick_volume] [spread] [real_volume]
   [0] 2022.09.06 04:00:00 0.99686 0.99708 0.99611 0.99641          4463        0             0
   [1] 2022.09.06 05:00:00 0.99638 0.99643 0.99491 0.99588          4519        0             0
   [2] 2022.09.06 06:00:00 0.99588 0.99591 0.99426 0.99441          3060        0             0
   [3] 2022.09.06 07:00:00 0.99441 0.99550 0.99441 0.99464          3867        0             0
   [4] 2022.09.06 08:00:00 0.99464 0.99652 0.99448 0.99594          5280        0             0
   [5] 2022.09.06 09:00:00 0.99594 0.99795 0.99494 0.99697          7227        0             0
   [6] 2022.09.06 10:00:00 0.99698 0.99865 0.99645 0.99758         10130        0             0
   [7] 2022.09.06 11:00:00 0.99758 0.99764 0.99472 0.99581          7012        0             0
   [8] 2022.09.06 12:00:00 0.99581 0.99604 0.99360 0.99528          6166        0             0
   [9] 2022.09.06 13:00:00 0.99528 0.99570 0.99220 0.99259          6950        0             0
   vector_rates.CopyRates COPY_RATES_OHLC failed. Error 4003
   vector_rates COPY_RATES_CLOSE:
   [0.9931,0.99293,0.99417,0.99504,0.9968399999999999,0.99641,0.99588,0.99441,0.99464,0.99594,0.99697,0.99758,0.99581,0.9952800000000001,0.99259]
*/

参见

访问时间序列和指标，CopyRates

7.2.4 CopyTicks

从 MqlTick 结构获取跳价数据并存储到矩阵或向量当中。元素顺序从过去到现在计数，这意味着索引为 0 的刻度是最久远的。 若要分析跳价，检查 flags 字段，其显示跳价中的确切变化。

bool  matrix::CopyTicks(
   string           symbol,                // 品名
   ulong            flags,                 // 指示欲接收跳价类型的标志
   ulong            from_msc,              // 欲请求跳价的起始时间
   ulong            count                  // 欲接收跳价的数量
   );

向量方法

bool  vector::CopyTicks(
   string           symbol,                // 品名
   ulong            flags,                 // 指示欲接收跳价类型的标志
   ulong            from_msc,              // 欲请求跳价的起始时间
   ulong            count                  // 欲接收跳价的数量
   );

参数

symbol

[输入] 品种。

flags

[输入] ENUM_COPY_TICKS 枚举中的标志组合，指示所请求数据的内容。当复制到向量时，只能从 ENUM_COPY_TICKS 枚举中指定一个值，否则会发生错误。

from_msc

[输入] 请求跳价的开始时间。 自 1970 年 01 月 01 日起，时间以毫秒为单位指定。 如果 from_msc=0，则返回等于 'count' 的最后跳价数字。

count

[输入] 所请求跳价的数量。 如果参数 'from_msc' 和 'count' 未指定，则将写入所有可用的跳价，但不超过 2000。

返回值

成功时返回 true，如果发生错误则 false。

注意

首次调用 CopyTicks() 会启动硬盘驱动器上存储的相关品种跳价数据库的同步。 如果本地数据库没有提供全部请求的跳价，则缺失的跳价将自动从交易服务器下载。 跳价的同步自 CopyTicks() 中指定的 from_msc 到当前时刻。 之后，该品种所有到达的跳价都将添加到跳价数据库之中，从而使其保持同步状态。

如果 from_msc 和 count 参数未指定，则把全部可用跳价，但不超过 2000 个，写入矩阵/向量之中。

在指标中，CopyTicks() 方法立即返回结果：当从指标调用时，CopyTick() 会立即返回品种的所有可用跳价，如果可用数据不足，则启动跳价数据库的同步。 同一品种上的所有指标都在一个公用线程中运行，因此指标不能等待同步完成。 同步后，CopyTicks() 将在下一次调用期间返回所有请求的跳价。 在指标中，OnCalculate() 函数在每次跳价到达后调用。

在智能系统和脚本中，CopyTicks() 可以等待结果 45 秒：与指标不同，每个智能系统或脚本都在单独的线程中运行，因此为完成同步最多可以等待 45 秒。 如果在此期间无法同步所需数量的跳价，CopyTicks() 将在超时后返回可用的跳价，并继续同步。 智能系统里的 OnTick() 并非每次跳价都会处理，它只通知智能系统行情有所变化。 这可能是一批变化：终端可以同时接收多次跳价，而 OnTick() 只会调用一次，通知智能系统最新的行情状态。

数据返回率：终端在高速访问缓存中为每个金融产品存储了 4096 个最后的跳价（市场深度为运营品种存储 65536 个跳价）。 有关此数据的请求执行速度最快。 如果当前交易时段请求的跳价超出缓存，CopyTicks() 将调用存储在终端内存中的跳价。 这些请求需要更多时间才能完成。 最慢的请并非那些请求其它日期的跳价，因为在这种情况下，数据是从驱动器读取的。

ENUM_COPY_TICKS

ENUM_COPY_TICKS 枚举包含指定要传递给矩阵或数组的数据类型的标志。 标志组合允许在一个请求中从历史记录中获取多个序列。 矩阵中行的顺序将与 ENUM_COPY_TICKS 枚举中数值的顺序相对应。 换言之，含有最高价数据的行在矩阵中将始终高于含有最低价数据的行。

ID	值	说明
COPY_TICKS_INFO	1	包含卖价（Bid）和/或买价（Ask）价格变化的报价
COPY_TICKS_TRADE	2	包含最后价（Last）和/或交易量（Volume）价格变化的报价
COPY_TICKS_ALL	3	所有报价
COPY_TICKS_TIME_MS	1<<8	跳价时间（以毫秒为单位）
COPY_TICKS_BID	1<<9	出价（Bid）
COPY_TICKS_ASK	1<<10	要价（Ask）
COPY_TICKS_LAST	1<<11	最后价（最后成交价）
COPY_TICKS_VOLUME	1<<12	最后价交易量
COPY_TICKS_FLAGS	1<<13	跳价标志
数据排列
COPY_TICKS_VERTICAL	32768	报价沿垂直轴复制到矩阵中。接收到的报价将在矩阵中垂直排列，即最早的报价将位于第一行，而最新的报价将位于矩阵的最后一行。 使用默认复制时，报价会沿水平轴添加到矩阵中。 该标识仅在复制到矩阵时适用。

分析跳价标志以便找出哪些数据已变化：

• TICK_FLAG_BID ― 跳价改变了出价
• TICK_FLAG_ASK ― 跳价改变了要价
• TICK_FLAG_LAST ― 跳价改变了最后成交价
• TICK_FLAG_VOLUME ― 跳价改变了交易量
• TICK_FLAG_BUY ― 跳价是买入成交的结果
• TICK_FLAG_SELL ― 跳价是卖出成交的结果

参见

访问时间序列和指标，CopyTicks

7.2.5 CopyTicksRange

按指定日期范围，获取 MqlTick 结构的跳价，并存储到矩阵或向量之中。 元素顺序从过去到现在计数，这意味着索引为 0 的跳价是最久远的。 若要分析跳价，检查 flags 字段，其显示跳价中的确切变化。

bool  matrix::CopyTicksRange(
   string           symbol,                // 品名
   ulong            flags,                 // 指示欲接收跳价类型的标志
   ulong            from_msc,              // 欲请求跳价的起始时间
   ulong            to_msc                 // 欲请求跳价的截止时间
   );

向量方法

bool  vector::CopyTicksRange(
   string           symbol,                // 品名
   ulong            flags,                 // 指示欲接收跳价类型的标志
   ulong            from_msc,              // 欲请求跳价的起始时间
   ulong            to_msc                 // 欲请求跳价的截止时间
   );

参数

symbol

[输入] 品种。

flags

[输入] ENUM_COPY_TICKS 枚举中的标志组合，指示所请求数据的内容。当复制到向量时，只能从 ENUM_COPY_TICKS 枚举中指定一个值，否则会发生错误。

from_msc

[输入] 请求跳价的开始时间。 自 1970 年 01 月 01 日起，时间以毫秒为单位指定。 如果未指定 “from_msc” 参数，则跳价从头开始返回历史记录。 即返回时间 >= from_msc 的跳价。

to_msc

[输入] 请求截止的跳价时间。 自 1970 年 01 月 01 日起，时间以毫秒为单位指定。 返回时间 <= to_msc 的跳价。 如果未指定 to_msc 参数，则返回截至历史记录结束之前的所有跳价。

返回值

成功时返回 true，如果发生错误则返回 false。 GetLastError() 能返回以下错误:

• ERR_HISTORY_TIMEOUT ― 跳价同步的超时已过期，函数返回它已拥有的一切。
• ERR_HISTORY_SMALL_BUFFER ― 静态缓存区太小。 仅返回数组可以存储的数量。
• ERR_NOT_ENOUGH_MEMORY ― 内存不足，无法将指定范围的历史数据接收到动态跳价数组之中。为跳价数组分配足够内存失败。

分析跳价标志以便找出哪些数据已变化：

• TICK_FLAG_BID ― 跳价改变了出价
• TICK_FLAG_ASK ― 跳价改变了要价
• TICK_FLAG_LAST ― 跳价改变了最后成交价
• TICK_FLAG_VOLUME ― 跳价改变了交易量
• TICK_FLAG_BUY ― 跳价是买入成交的结果
• TICK_FLAG_SELL ― 跳价是卖出成交的结果

注意

CopyTicksRange() 方法请求的跳价精确到指定范围。 例如，历史记录中指定日期的跳价。 CopyTicks() 只允许指定开始日期，例如，接收从月初到现在的所有跳价。

参见

访问时间序列和指标，CopyTicksRange

7.2.6 Eye

统计函数。 构造具有指定大小的矩阵，主对角线上为 1，其它之处则为 0。 返回一个矩阵，对角线上为 1，其它之处为零。

static matrix matrix::Eye(
  const ulong  rows,        // 行数
  const ulong  cols,        // 列数
  const int    ndiag=0      // 对角线索引
   );

参数

rows

[输入] 输出中的行数。

cols

[输入] 输出中的列数。

ndiag=0

[输入] 对角线索引：0（默认值）表示主对角线，正值表示上对角线，负值表示下对角线。

返回值

所有元素都等于零的矩阵，但第 k 对角线除外，其值等于 1。

MQL5 示例:

  matrix eye=matrix::Eye(3, 3);
  Print("eye = \n", eye);
  
  eye=matrix::Eye(4, 4,1);
  Print("eye = \n", eye);  
  /*
   eye = 
   [[1,0,0]
    [0,1,0]
    [0,0,1]]
   eye = 
   [[0,1,0,0]
    [0,0,1,0]
    [0,0,0,1]
    [0,0,0,0]]   
  */

Python 示例:

np.eye(3, dtype=int)
array([[1, 0, 0],
       [0, 1, 0],
       [0, 0, 1]])
 
np.eye(4, k=1)
array([[0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.],
       [0., 0., 0., 0.]])

7.2.7 Identity

它是一个静态函数，可创建指定大小（不一定是正方形）的单位矩阵。 一个单位矩阵在主对角线上包含 0，在其它所在包含零。 主对角线由行索引和列索引相等的矩阵元素组成，譬如 [0,0]、[1,1]、[2,2]，等等。 创建一个新的单位矩阵。

还有一个 Identity 方法能将已经存在的矩阵转换为单位矩阵。

static matrix matrix::Identity(
  const ulong  rows,        // 行数
  const ulong  cols,        // 列数
   );
 
void matrix::Identity();

参数

rows

[输入] n x n 矩阵中的行数（和列数）。

返回值

返回单位矩阵。 单位矩阵是一个方阵，主对角线上为 1。

MQL5 示例:

  matrix identity=matrix::Identity(3,3);
  Print("identity = \n", identity);  
/* 
   identity = 
   [[1,0,0]
    [0,1,0]
    [0,0,1]]
*/
  matrix identity2(3,5);
  identity2.Identity();
  Print("identity2 = \n", identity2);  
/* 
   identity2 = 
   [[1,0,0,0,0]
    [0,1,0,0,0]
    [0,0,1,0,0]]
*/ 

Python 示例:

np.identity(3)
array([[1.,  0.,  0.],
       [0.,  1.,  0.],
       [0.,  0.,  1.]])

7.2.8 Ones

这是一个静态函数，创建并返回一个新矩阵，且以 1 填充。

static matrix matrix::Ones(
  const ulong  rows,     // 行数
  const ulong  cols      // 列数
   );
 
static vector vector::Ones(
  const ulong  size,     // 向量大小
   );

参数

rows

[输入] 行数。

cols

[输入] 列数。

返回值

给定行数和列数的新矩阵，且填充了 1。

MQL5 示例:

  matrix ones=matrix::Ones(4, 4);
  Print("ones = \n", ones);
/*
ones = 
   [[1,1,1,1]
    [1,1,1,1]
    [1,1,1,1]
    [1,1,1,1]]
*/

Python 示例:

np.ones((4, 1))
array([[1.],
       [1.]])

7.2.9 Zeros

这是一个静态函数，创建并返回一个填充零值的新矩阵。

static matrix matrix::Zeros(
  const ulong  rows,     // 行数
  const ulong  cols      // 列数
   );
 
static vector vector::Zeros(
  const ulong  size,     // 向量大小
   );

参数

rows

[输入] 行数。

cols

[输入] 列数。

返回值

给定行数和列数的新矩阵，并以零填充。

MQL5 示例:

  matrix zeros=matrix::Zeros(3, 4);
  Print("zeros = \n", zeros);
/*
zeros = 
   [[0,0,0,0]
    [0,0,0,0]
    [0,0,0,0]]
*/

Python 示例:

np.zeros((2, 1))
array([[ 0.],
       [ 0.]])

7.2.10 Full

静态函数创建并返回一个新矩阵，并按给定值填充。

static matrix matrix::Full(
  const ulong   rows,      // number or rows
  const ulong   cols,      // number of columns
  const double  value      // 填充值
   );
 
static vector vector::Full(
  const ulong   size,      // vector size
  const double  value      // 填充值
   );

参数

rows

[输入] 行数。

cols

[输入] 列数。

value

[输入] 填充所有矩阵元素的数值。

返回值

返回给定行和列的新矩阵，并用指定值填充。

MQL5 示例:

  matrix full=matrix::Full(3,4,10);
  Print("full = \n", full);
/*
full = 
   [[10,10,10,10]
    [10,10,10,10]
    [10,10,10,10]]
*/

举例

np.full((2, 2), 10)
array([[10, 10],
       [10, 10]])

7.2.11 Tri

这是一个构造矩阵的静态函数，其中给定对角线为 1，，且其它地方为 0。

static matrix matrix::Tri(
  const ulong rows,        // 行数
  const ulong cols,        // 列数
  const int   ndiag=0      // 对角线数
   );

参数

rows

[输入] 数组中的行数。

cols

[输入] 数组中的列数。

ndiag=0

[输入] 子对角线及其下方数组被填充。 k = 0 是主对角线，而 k < 0 在其下方，k > 0 在上方。 默认填充值为 0。

返回值

数组，其下三角以 1 填充，在其它所在则填充 0。

MQL5 示例:

   matrix matrix_a=matrix::Tri(3,4,1);
   Print("Tri(3,4,1)\n",matrix_a);
   matrix_a=matrix::Tri(4,3,-1);
   Print("Tri(4,3,-1)\n",matrix_a);
 
/*
   Tri(3,4,1)
   [[1,1,0,0]
    [1,1,1,0]
    [1,1,1,1]]
   Tri(4,3,-1)
   [[0,0,0]
    [1,0,0]
    [1,1,0]
    [1,1,1]]
*/

举例

np.tri(3, 5, 2, dtype=int)
array([[1, 1, 1, 0, 0],
       [1, 1, 1, 1, 0],
       [1, 1, 1, 1, 1]])

7.2.12 Init

初始化矩阵或向量。

void matrix::Init(
  const ulong  rows,            // 行数
  const ulong  cols,            // 列数
  func_name    init_func=NULL,  // 置于类的某个作用域或静态方法中的 init 函数
   ...         parameters
   );
 
void vector::Init(
  const ulong  size,            // 向量大小
  func_name    init_func=NULL,  // 置于类的某个作用域或静态方法中的 init 函数
   ...         parameters
   );

参数

rows

[输入] 行数。

cols

[输入] 列数。

func_name

[输入] 初始化函数。

...

[输入] 初始化函数的参数。

返回值

无返回值。

举例

template<typename T>
void MatrixArange(matrix<T> &mat,T value=0.0,T step=1.0)
  {
   for(ulong i=0; i<mat.Rows(); i++)
     {
      for(ulong j=0; j<mat.Cols(); j++,value+=step)
         mat[i][j]=value;
     }
  }
template<typename T>
void VectorArange(vector<T> &vec,T value=0.0,T step=1.0)
  {
   for(ulong i=0; i<vec.Size(); i++,value+=step)
      vec[i]=value;
  }
//+------------------------------------------------------------------+
//| 脚本程序 start 函数                                                |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
  int size_m=3, size_k=4;
  matrix  m(size_m,size_k,MatrixArange,-2.,0.1); // 首先创建一个大小为 size_ m x size_k 的未初始化矩阵，
  Print("matrix m \n",m);                        // 然后调用初始化清单列出的带参数的 MatrixArange 函数
  matrixf m_float(5,5,MatrixArange,-2.f,0.1f);   // 创建浮点型矩阵后，调用 MatrixArange 函数
  Print("matrix m_float \n",m_float);
  vector  v(size_k,VectorArange,-10.0);          // 创建一个向量后，会调用带有一个参数的 VectorArange；其第二个参数采用默认值
  Print("vector v \n",v);  
  /*
   matrix m 
   [[-2,-1.9,-1.8,-1.7]
    [-1.6,-1.5,-1.399999999999999,-1.299999999999999]
    [-1.199999999999999,-1.099999999999999,-0.9999999999999992,-0.8999999999999992]]
   matrix m_float 
   [[-2,-1.9,-1.8,-1.6999999,-1.5999999]
    [-1.4999999,-1.3999999,-1.2999998,-1.1999998,-1.0999998]
    [-0.99999976,-0.89999974,-0.79999971,-0.69999969,-0.59999967]
    [-0.49999967,-0.39999968,-0.29999968,-0.19999969,-0.099999689]
    [3.1292439e-07,0.10000031,0.20000032,0.30000031,0.4000003]]
   vector v 
   [-10,-9,-8,-7]
  */ 
  }

7.2.13 Fill

用指定的数值填充存在的矩阵或向量。

void matrix::Fill(
  const double  value      // 填充值
   );
 
void vector::Fill(
  const double  value      // 填充值
   );

参数

value

[输入] 填充所有矩阵元素的数值。

返回值

无返回值。 矩阵将用指定的值填充。

举例

   matrix matrix_a(2,2);
   matrix_a.Fill(10);
   Print("matrix_a\n",matrix_a);
 
/*
  matrix_a
  [[10,10]
   [10,10]]
*/

7.3 矩阵和向量操纵

这些是基本矩阵操作的方法：填充、复制、获取矩阵的一部分、转置、拆分和排序。

还有若干种方法可针对矩阵的行和列进行操纵。

函数	动作
HasNan	返回矩阵/向量中NaN值的数量
Transpose	反转或置换矩阵的轴；返回修改后的矩阵
TriL	返回矩阵的副本，其中第 k 个对角线以上的元素归零。 下三角矩阵
TriU	返回矩阵的副本，其中第 k 对角线以下的元素归零。 上三角矩阵
Diag	提取对角线或构造对角矩阵
Row	返回行向量。 写入向量指定行
Col	返回列向量。 写入向量指定列。
Copy	返回给定矩阵/向量的副本
Compare	以指定的精度比较两个矩阵/向量的元素
CompareByDigits	比较两个矩阵/向量的元素，直至有效位数
Flat	允许依据一个索引替代两个索引定位矩阵元素
Clip	将矩阵/向量的元素限制为指定范围内的有效值
Reshape	在不更改矩阵数据的情况下更改矩阵的形状
Resize	返回形状和大小均已更改的新矩阵
SwapRows	交换矩阵中的行
SwapCols	交换矩阵中的列
Split	将矩阵拆分为多个子矩阵
Hsplit	将矩阵水平拆分为多个子矩阵。 与 轴=0 的 Split 相同
Vsplit	将矩阵垂直拆分为多个子矩阵。 与 axis=1 的拆分相同
ArgSort	间接针对矩阵或向量进行排序。
Sort	就地针对矩阵或向量进行排序。

7.3.1 HasNan

返回矩阵/向量中NaN值的数量。

ulong vector::HasNan();
 
ulong matrix::HasNan();

返回值

包含NaN值的矩阵/向量元素数。

注意

当比较具有NaN值的相应元素对时，Compare和CompareByDigits方法认为这些元素相等，而在通常比较浮点数NaN != NaN的情况下。

例如：

void OnStart(void)
  {
   double x=sqrt(-1);
 
   Print("single: ",x==x);
 
   vector<double> v1={x};
   vector<double> v2={x};
 
   Print("vector: ", v1.Compare(v2,0)==0);
  }
 
/* Result:
 
 single: false
 vector: true
*/

另见

MathClassify，Compare， CompareByDigits

7.3.2 Transpose

矩阵转置。 反转或排列矩阵的轴；返回修改后的矩阵。

matrix matrix::Transpose()

返回值

转置后的矩阵。

以 MQL5 实现的简单矩阵转置算法：

matrix MatrixTranspose(const matrix& matrix_a)
  {
   matrix matrix_c(matrix_a.Cols(),matrix_a.Rows());
 
   for(ulong i=0; i<matrix_c.Rows(); i++)
      for(ulong j=0; j<matrix_c.Cols(); j++)
         matrix_c[i][j]=matrix_a[j][i];
 
   return(matrix_c);
  }

MQL5 示例:

  matrix a= {{0, 1, 2}, {3, 4, 5}};
  Print("matrix a \n", a);
  Print("a.Transpose() \n", a.Transpose());
 
  /*
  matrix a
  [[0,1,2]
   [3,4,5]]
  a.Transpose()
  [[0,3]
   [1,4]
   [2,5]]
  */

Python 示例:

import numpy as np
 
a = np.arange(6).reshape((2,3))
print("a \n",a)
print("np.transpose(a) \n",np.transpose(a))
 
a 
 [[0 1 2]
 [3 4 5]]
np.transpose(a) 
 [[0 3]
 [1 4]
 [2 5]]

7.3.3 TriL

返回矩阵的副本，其中第 k 个对角线以上的元素归零。 下三角矩阵。

matrix matrix::Tril(
  const int     ndiag=0      // 对角线的索引
   );

参数

ndiag=0

[输入] 对角线，高于该对角线的元素为零。 ndiag = 0（默认值）是主对角线，ndiag < 0 在其下方，ndiag > 0 位于其上方。

返回值

数组，其下三角以 1 填充，在其它所在则填充 0。

MQL5 示例:

   matrix a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   matrix b=a.TriL(-1);
   Print("matrix b \n",b);
 
  /*
  matrix_c
  [[0,0,0]
  [4,0,0]
  [7,8,0]
  [10,11,12]]
  */

Python 示例:

import numpy as np
 
a=np.tril([[1,2,3],[4,5,6],[7,8,9],[10,11,12]], -1)
 
[[ 0  0  0]
 [ 4  0  0]
 [ 7  8  0]
 [10 11 12]]

7.3.4 TriU

返回矩阵的副本，其中第 k 个对角线下方的元素归零。 上三角形矩阵。

matrix matrix::Triu(
  const int     ndiag=0      // 对角线的索引
   );

参数

ndiag=0

[输入] 对角线之下的元素为零。 ndiag = 0（默认值）是主对角线，ndiag < 0 在其下方，ndiag > 0 位于其上方。

MQL5 示例:

   matrix a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   matrix b=a.TriU(-1);
   Print("matrix b \n",b);
 
  /*
  matrix b
  [[1,2,3]
   [4,5,6]
   [0,8,9]
   [0,0,12]]
  */

Python 示例:

import numpy as np
 
a=np.triu([[1,2,3],[4,5,6],[7,8,9],[10,11,12]], -1)
print(a)
 
[[ 1  2  3]
 [ 4  5  6]
 [ 0  8  9]
 [ 0  0 12]]

7.3.5 Diag

提取对角或构造对角矩阵。

vector matrix::Diag(
  const int     ndiag=0      // 对角线数
   );
 
void matrix::Diag(
  const vector  v,           // 对角线向量
  const int     ndiag=0      // 对角线数
   );

参数

v

[输入] 一个向量，其元素将包含在相应的对角线中（ndiag=0 是主对角线）。

ndiag=0

[输入] 问题中的对角。 默认填充值为 0。 对于主对角线上方的对角线使用 ndiag>0，对于主对角线下方的对角线使用 ndiag<0。

注意

未分配的矩阵（没有维度）亦可设置对角线。 在这种情况下，将创建一个大小为零矩阵，其大小对应于对角向量的大小，之后向量值将填充到相应的对角线中。 如果为已存在的矩阵设置对角线，则矩阵尺寸不会更改，且对角线向量外的矩阵元素值也不会更改。

举例

   vector v1={1,2,3};
   matrix m1;
   m1.Diag(v1);
   Print("m1\n",m1);
   matrix m2;
   m2.Diag(v1,-1);
   Print("m2\n",m2);
   matrix m3;
   m3.Diag(v1,1);
   Print("m3\n",m3);
   matrix m4=matrix::Full(4,5,9);
   m4.Diag(v1,1);
   Print("m4\n",m4);
   
   Print("diag -1 - ",m4.Diag(-1));
   Print("diag 0 - ",m4.Diag());
   Print("diag 1 - ",m4.Diag(1));
 
  /*
 
  m1
  [[1,0,0]
  [0,2,0]
  [0,0,3]]
  m2
  [[0,0,0]
  [1,0,0]
  [0,2,0]
  [0,0,3]]
  m3
  [[0,1,0,0]
  [0,0,2,0]
  [0,0,0,3]]
  m4
  [[9,1,9,9,9]
  [9,9,2,9,9]
  [9,9,9,3,9]
  [9,9,9,9,9]]
  diag -1 - [9,9,9]
  diag 0 - [9,9,9,9]
  diag 1 - [1,2,3,9]
  */

7.3.6 Row

返回行向量。 写入向量指定行

vector matrix::Row(
  const ulong   nrow      // 行号
   );
 
void matrix::Row(
  const vector  v,        // 行向量
  const ulong   nrow      // 行号
   );

参数

nrow

[输入] 行号。

返回值

向量。

注意

可以为未分配的矩阵（没有维度）设置行。 在这种情况下，将创建一个零矩阵，其大小为向量大小 x 行数+1，之后向量元素的值将填充在相应的行中。 如果为已存在的矩阵设置行，则矩阵维度不会更改，行向量之外的矩阵元素的值也不会更改。

举例

   vector v1={1,2,3};
   matrix m1;
   m1.Row(v1,1);
   Print("m1\n",m1);
   matrix m2=matrix::Full(4,5,7);
   m2.Row(v1,2);
   Print("m2\n",m2);
   
   Print("row 1 - ",m2.Row(1));
   Print("row 2 - ",m2.Row(2));
 
  /*
  m1
  [[0,0,0]
  [1,2,3]]
  m2
  [[7,7,7,7,7]
  [7,7,7,7,7]
  [1,2,3,7,7]
  [7,7,7,7,7]]
  row 1 - [7,7,7,7,7]
  row 2 - [1,2,3,7,7]
  */

7.3.7 Col

返回列向量。 将向量写入指定的列。

vector matrix::Col(
  const ulong   ncol      // 列号
   );
 
void matrix::Col(
  const vector  v,        // 列向量
  const ulong   ncol      // 列号
   );

参数

ncol

[输入] 列数。

返回值

向量。

注意

可以为未分配的矩阵（没有维度）设置列数。 在这种情况下，将创建一个零矩阵，其大小为向量大小 x 列数+1，之后向量元素的值将填充在相应的列中。 如果为已存在的矩阵设置列，则矩阵维度不会变化，且列向量之外的矩阵元素值亦不会变化。

举例

   vector v1={1,2,3};
   matrix m1;
   m1.Col(v1,1);
   Print("m1\n",m1);
   matrix m2=matrix::Full(4,5,8);
   m2.Col(v1,2);
   Print("m2\n",m2);
   
   Print("col 1 - ",m2.Col(1));
   Print("col 2 - ",m2.Col(2));
 
  /*
  m1
  [[0,1]
  [0,2]
  [0,3]]
  m2
  [[8,8,1,8,8]
  [8,8,2,8,8]
  [8,8,3,8,8]
  [8,8,8,8,8]]
  col 1 - [8,8,8,8]
  col 2 - [1,2,3,8]
  */

7.3.8 Copy

创建给定矩阵/向量的副本。

bool matrix::Copy(
  const matrix&  a     // 复制的矩阵
   );
bool vector::Copy(
  const vector&  v     // 复制的向量
   );

参数

v

[输入] 欲复制的矩阵或矢量。

返回值

成功时返回 true，否则返回 false。

MQL5 示例:

  matrix a=matrix::Eye(3, 4);
  matrix b;
  b.Copy(a);
  matrix c=a;
  Print("matrix b \n", b);
  Print("matrix_c \n", c);
 
  /*
  /*
  matrix b
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]]
  matrix_c
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]]
  */
  */

Python 示例:

import numpy as np
 
a = np.eye(3,4)
print('a \n',a)
b = a
print('b \n',b)
c = np.copy(a)
print('c \n',c)
 
a 
 [[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]]
b 
 [[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]]
c 
 [[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]]

7.3.9 Compare

按指定的精度比较两个矩阵/向量的元素。

ulong vector::Compare(
  const vector& vec,         // 欲比较的向量
  const double  epsilon       // 精度
   );
 
ulong matrix::Compare(
  const matrix& mat,          // 欲比较的矩阵
  const double  epsilon       // 精度
   );

参数

vector_b

[输入] 欲比较的向量。

epsilon

[输入] 精度。

返回值

所比较的矩阵或向量的不匹配元素数量：如果矩阵相等，则为 0，否则大于 0。

注意

比较运算符 == 或 != 执行精确的元素级比较。 众所周知，实数的精确比较用途有限，因此增加了 epsilon 比较方法。 一个矩阵也许包含某个范围内的元素，例如从 1e-20 到 1e+20。 这些矩阵可逐元素比较来进行处理，直到有效数字。

对于复数矩阵/向量，该比较包括估计复数之间的距离。距离的计算公式为sqrt(pow(r1-r2, 2) + pow(i1-i2, 2)，并且是一个可以与epsilon进行比较的实数。

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4}};
   matrix matrix_i=matrix::Identity(3,3);
   matrix matrix_c=matrix_a.Inv();
   matrix matrix_check=matrix_a.MatMul(matrix_c);
   Print("matrix_check\n",matrix_check);
 
   ulong errors=matrix_check.Compare(matrix::Identity(3,3),1e-15);
   Print("errors=",errors);
 
 
  /*
  matrix_check
  [[1,0,0]
  [4.440892098500626e-16,1,8.881784197001252e-16]
  [4.440892098500626e-16,2.220446049250313e-16,0.9999999999999996]]
  errors=0
 
  */

7.3.10 CompareByDigits

按有效位数精度比较两个矩阵/向量的元素。

ulong vector::CompareByDigits(
  const vector& vec,          // 欲比较的向量
  const int     digits        // 有效位数
   );
 
ulong matrix::CompareByDigits(
  const matrix& mat,          // 欲比较的矩阵
  const int     digits        // 有效位数
   );

参数

vector_b

[输入] 欲比较的向量。

digits

[输入] 进行比较采用的有效位数。

epsilon

[输入] 比较精度。 如果两个值的绝对值相差小于指定的精度，则认为它们相等。

返回值

所比较的矩阵或向量的不匹配元素数量：如果矩阵相等，则为 0，否则大于 0。

注意

比较运算符 == 或 != 执行精确的元素级比较。 众所周知，实数的精确比较用途有限，因此增加了 epsilon 比较方法。 一个矩阵也许包含某个范围内的元素，例如从 1e-20 到 1e+20。 此类矩阵可用元素级比较来处理，直至有效位数。

举例

   int    size_m=128;
   int    size_k=256;
   matrix matrix_a(size_m,size_k);
//--- 填充矩阵
   double  value=0.0;
   for(int i=0; i<size_m; i++)
     {
      for(int j=0; j<size_k; j++)
        {
         if(i==j)
            matrix_a[i][j]=1.0+i;
         else
           {
            value+=1.0;
            matrix_a[i][j]=value/1e+20;
           }
        }
     }
//--- 获取其它矩阵
   matrix matrix_c = matrix_a * -1;
 
   ulong errors_epsilon=matrix_a.Compare(matrix_c,1e-15);
   ulong errors_digits=matrix_a.CompareByDigits(matrix_c,15);
 
   printf("Compare matrix %d x %d  errors_epsilon=%I64u  errors_digits=%I64u",size_m,size_k,errors_epsilon,errors_digits);
 
 
  /*
  比较 矩阵 128 x 256  errors_epsilon=128  errors_digits=32768
  */

7.3.11 Flat

允许依据一个索引替代两个索引来定位对矩阵元素。

bool matrix::Flat(
  const ulong   index,     // 
  const double  value      // 设置的数值
   );
 
double matrix::Flat(
  const ulong   index,     // 
   );

参数

index

[输入] 寻址索引

value

[输入] 给定索引值。

返回值

依据给定索引得到的值。

注意

对于矩阵 mat(3,3)，访问可以写成如下：

• 读取: 'x=mat.Flat(4)', 其等效于 'x=mat[1][1]'
• 写入: 'mat.Flat(5, 42)', 等效于 'mat[1][2]=42'

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
   ulong arg_max=matrix_a.ArgMax();
   Print("max_value=",matrix_a.Flat(arg_max));
   matrix_a.Flat(arg_max,0);
   arg_max=matrix_a.ArgMax();
   Print("max_value=",matrix_a.Flat(arg_max));
 
 
  /*
  matrix_a
  [[10,3,2]
   [1,8,12]
   [6,5,4]
   [7,11,9]]
  max_value=12.0
  max_value=11.0
  */

7.3.12 Clip

将矩阵/向量的元素限制在指定的有效值范围内。

bool matrix::Clip(
  const double  min_value,     // 最小值
  const double  max_value      // 最大值
   );
bool vector::Clip(
  const double  min_value,     // 最小值
  const double  max_value      // 最大值
   );

参数

min_value

[输入] 最小值。

max_value

[输入] 最大值。

返回值

成功时返回 true，否则返回 false。

注意

矩阵（或向量）就地处理。 不会创建任何副本。

举例

   matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   bool res=matrix_a.Clip(4,8);
   Print("matrix_a\n",matrix_a);
 
  /*
  matrix_a
  [[4,4,4]
   [4,5,6]
   [7,8,8]
   [8,8,8]]
  */

7.3.13 Reshape

在不更改其数据的情况下更改矩阵的形状。

void  Reshape(
  const ulong  rows,     // 新的行数。
  const ulong  cols      // 新的列数。
   );

参数

rows

[输入] 新的行数.

cols

[输入] 新的列数.

注意

矩阵就地处理。 不会创建任何副本。 可以指定任何大小，即，rows_newcols_new!=rows_oldcols_old。 当矩阵缓冲区增加时，额外数值均未定义。

举例

   matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
 
   Print("matrix_a\n",matrix_a);
   matrix_a.Reshape(2,6);
   Print("Reshape(2,6)\n",matrix_a);
   matrix_a.Reshape(3,5);
   Print("Reshape(3,5)\n",matrix_a);
   matrix_a.Reshape(2,4);
   Print("Reshape(2,4)\n",matrix_a);
 
  /*
  matrix_a
  [[1,2,3]
   [4,5,6]
   [7,8,9]
   [10,11,12]]
  Reshape(2,6)
  [[1,2,3,4,5,6]
   [7,8,9,10,11,12]]
  Reshape(3,5)
  [[1,2,3,4,5]
   [6,7,8,9,10]
   [11,12,0,3,0]]
  Reshape(2,4)
  [[1,2,3,4]
   [5,6,7,8]]
  */

7.3.14 Resize

返回已更改形状和大小的新矩阵。

bool matrix::Resize(
  const ulong  rows,     // 
  const ulong  cols,     // 新列数。
  const ulong  reserve=0 // 项目保留额度。
   );
 
bool vector::Resize(
  const ulong  size,     // 新大小。
  const ulong  reserve=0 // 项目保留额度。
   );

参数

rows

[输入] 新的行数.

cols

[输入] 新的列数.

返回值

成功时返回 true，否则返回 false。

注意

矩阵（或向量）就地处理。 不会创建任何副本。 可以指定任何大小，即，rows_newcols_new!=rows_oldcols_old。 与 Reshape 不同，矩阵是逐行处理的。 当增加列数时，额外列的数值均未定义。 当增加行数时，额外行的数值均未定义。 当减少列数时，矩阵的每一行都会被截断。

举例

   matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
   matrix_a.Resize(2,6);
   Print("Ressize(2,6)\n",matrix_a);
   matrix_a.Resize(3,5);
   Print("Resize(3,5)\n",matrix_a);
   matrix_a.Resize(2,4);
   Print("Resize(2,4)\n",matrix_a);
 
   /*
   matrix_a
   [[1,2,3]
    [4,5,6]
    [7,8,9]
    [10,11,12]]
   Ressize(2,6)
   [[1,2,3,4,5,6]
    [4,5,6,10,11,12]]
   Resize(3,5)
   [[1,2,3,4,5]
    [4,5,6,10,11]
    [11,12,3,8,8]]
   Resize(2,4)
   [[1,2,3,4]
    [4,5,6,10]]
   */

7.3.15 Set

根据指定索引设置向量元素值。

bool vector::Set(
  ulong   index,     // 元素索引
  double  value      // 值
   );

参数

index

[in] 需要为其设置值的元素索引。

值

[in] 值。

返回值

如果成功返回true，否则返回false。

注意

Set方法的作用与使用方括号赋值的作用相同，即：vector[index]=value. 添加该方法是为了简化从使用此类符号的语言中传递代码的过程。下面的示例显示了按指定索引用值填充向量的两个选项。

示例：

void OnStart()
  {
//---
   vector v1(10, VectorAssignValues);
   Print("v1 = ", v1);
 
   vector v2(10, VectorSetValues);
   Print("v2 = ", v2);
  }
 /* Result
  v1 = [1,2,4,8,16,32,64,128,256,512]
  v2 = [1,2,4,8,16,32,64,128,256,512]
  */
//+-------------------------------------------------------------------------+
//| 通过赋值运算用数字的幂填充向量                                              |
//+-------------------------------------------------------------------------+
void VectorAssignValues(vector& v, double initial=1)
  {
   double value=initial;
   for(ulong k=0; k<v.Size(); k++)
     {
      v[k]=value;
      value*=2;
     }
  }
//+--------------------------------------------------------------------------+
//| 使用Set方法用数字的幂填充向量                                                |
//+--------------------------------------------------------------------------+
void VectorSetValues(vector& v, double initial=1)
  {
   double value=initial;
   for(ulong k=0; k<v.Size(); k++)
     {
      v.Set(k, value);
      value*=2;
     }
  }

7.3.16 SwapRows

交换矩阵中的行。

bool matrix::SwapRows(
  const ulong  row1,     // 第一行的索引
  const ulong  row2      // 第二行的索引
   );

参数

row1

[输入] 第一个行的索引。

row2

[输入] 第二个行的索引。

返回值

成功时返回 true，否则返回 false。

举例

   matrix matrix_a={{1,2,3,4},
                    {5,6,7,8},
                    {9,10,11,12},
                    {13,14,15,16}};
   matrix matrix_i=matrix::Identity(4,4);
   matrix matrix_a1=matrix_a;
   matrix_a1.SwapRows(0,3);
   Print("matrix_a1\n",matrix_a1);
 
   matrix matrix_p=matrix_i;
   matrix_p.SwapRows(0,3);
   matrix matrix_c1=matrix_p.MatMul(matrix_a);
   Print("matrix_c1\n",matrix_c1);
 
  /*
  matrix_a1
  [[13,14,15,16]
   [5,6,7,8]
   [9,10,11,12]
   [1,2,3,4]]
  matrix_c1
  [[13,14,15,16]
   [5,6,7,8]
   [9,10,11,12]
   [1,2,3,4]]
  */

7.3.17 SwapCols

交换矩阵中的列。

bool matrix::SwapCols(
  const ulong  row1,     // 第一列的索引
  const ulong  row2      // 第二列的索引
   );

参数

col1

[输入] 第一个列的索引。

col2

[输入] 第二个列的索引。

返回值

成功时返回 true，否则返回 false。

举例

   matrix matrix_a={{1,2,3,4},
                    {5,6,7,8},
                    {9,10,11,12},
                    {13,14,15,16}};
   matrix matrix_i=matrix::Identity(4,4);
   matrix matrix_a1=matrix_a;
   matrix_a1.SwapCols(0,3);
   Print("matrix_a1\n",matrix_a1);
 
   matrix matrix_p=matrix_i;
   matrix_p.SwapCols(0,3);
   matrix matrix_c1=matrix_a.MatMul(matrix_p);
   Print("matrix_c1\n",matrix_c1);
 
  /*
  matrix_a1
  [[4,2,3,1]
   [8,6,7,5]
   [12,10,11,9]
   [16,14,15,13]]
  matrix_c1
  [[4,2,3,1]
   [8,6,7,5]
   [12,10,11,9]
   [16,14,15,13]]
  */

7.3.18 Split

将矩阵拆分为多个子矩阵。

bool matrix::Split(
  const ulong  parts,      // 子矩阵数
  const int    axis,       // 轴
  matrix&      splitted[]  // 结果子矩阵数组
   );
 
void matrix::Split(
  const ulong& parts[],    // 子矩阵大小
  const int    axis,       // 轴
  matrix&      splitted[]  // 结果子矩阵数组
   );

参数

parts

[输入] 欲将矩阵划分为子矩阵的数量。

axis

[输入] 轴。 0 - 水平轴，1 - 垂直轴。

splitted

[输出] 生成的子矩阵数组。

返回值

成功时返回 true，否则返回 false。

注意

如果指定了子矩阵的数量，则得到的子矩阵相同大小。 这意味着矩阵大小（0 - 行数，1 - 列数）必须能被 “parts” 参数整除，没有余数。 也可按子矩阵尺寸数组得到 不同尺寸的子矩阵。 各尺寸数组的元素都可用，直到整个矩阵被分割。 如果数组尺寸分割结束，而矩阵尚有部分未除尽，则未分割的余数将作为最后一个子矩阵。

举例

   matrix matrix_a={{ 1, 2, 3, 4, 5, 6},
                    { 7, 8, 9,10,11,12},
                    {13,14,15,16,17,18},
                    {19,20,21,22,23,24},
                    {25,26,27,28,29,30}};
   matrix splitted[];
   ulong  parts[]={2,2};
 
   bool res=matrix_a.Split(2,0,splitted);
   Print(res,"  ",GetLastError());
   ResetLastError();
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
 
   res=matrix_a.Split(2,1,splitted);
   Print(res,"  ",GetLastError());
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
 
   res=matrix_a.Split(parts,0,splitted);
   Print(res,"  ",GetLastError());
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
 
  /*
  false  4003
  true  0
  splitted 0
  [[1,2,3]
   [7,8,9]
   [13,14,15]
   [19,20,21]
   [25,26,27]]
  splitted 1
  [[4,5,6]
   [10,11,12]
   [16,17,18]
   [22,23,24]
   [28,29,30]]
  true  0
  splitted 0
  [[1,2,3,4,5,6]
   [7,8,9,10,11,12]]
  splitted 1
  [[13,14,15,16,17,18]
   [19,20,21,22,23,24]]
  splitted 2
  [[25,26,27,28,29,30]]
  */

7.3.18 Hsplit

将矩阵水平拆分为多个子矩阵。 与 axis=0 的拆分相同

bool matrix::Hsplit(
  const ulong  parts,      // 子矩阵数
  matrix&      splitted[]  // 结果子矩阵数组
   );
 
void matrix::Hsplit(
  const ulong& parts[],    // 子矩阵大小
  matrix&      splitted[]  // 结果子矩阵数组
   );

参数

parts

[输入] 欲将矩阵划分为子矩阵的数量。

splitted

[输出] 生成的子矩阵数组。

返回值

成功时返回 true，否则返回 false。

注意

如果指定了子矩阵的数量，则得到的子矩阵相同大小。 这意味着行数必须能被 “parts” 参数整除，没有余数。 也可按子矩阵尺寸数组得到 不同尺寸的子矩阵。 各尺寸数组的元素都可用，直到整个矩阵被分割。 如果数组尺寸分割结束，而矩阵尚有部分未除尽，则未分割的余数将作为最后一个子矩阵。

举例

   matrix matrix_a={{ 1, 2, 3, 4, 5, 6},
                    { 7, 8, 9,10,11,12},
                    {13,14,15,16,17,18},
                    {19,20,21,22,23,24},
                    {25,26,27,28,29,30}};
   matrix splitted[];
   ulong  parts[]={2,4};
 
   bool res=matrix_a.Hsplit(2,splitted);
   Print(res,"  ",GetLastError());
   ResetLastError();
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
 
   res=matrix_a.Hsplit(5,splitted);
   Print(res,"  ",GetLastError());
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
 
   res=matrix_a.Hsplit(parts,splitted);
   Print(res,"  ",GetLastError());
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
 
 
  /*
  false  4003
  true  0
  splitted 0
  [[1,2,3,4,5,6]]
  splitted 1
  [[7,8,9,10,11,12]]
  splitted 2
  [[13,14,15,16,17,18]]
  splitted 3
  [[19,20,21,22,23,24]]
  splitted 4
  [[25,26,27,28,29,30]]
  true  0
  splitted 0
  [[1,2,3,4,5,6]
  [7,8,9,10,11,12]]
  splitted 1
  [[13,14,15,16,17,18]
  [19,20,21,22,23,24]
  [25,26,27,28,29,30]]
  */

7.3.19 Vsplit

将矩阵垂直拆分为多个子矩阵。 axis=1 的拆分相同

bool matrix::Vsplit(
  const ulong  parts,      // 子矩阵数
  matrix&      splitted[]  // 结果子矩阵数组
   );
 
void matrix::Vsplit(
  const ulong& parts[],    // 子矩阵大小
  matrix&      splitted[]  // 结果子矩阵数组
   );

参数

parts

[输入] 欲将矩阵划分为子矩阵的数量。

7.3.20 splitted

[输出] 生成的子矩阵数组。

返回值

成功时返回 true，否则返回 false。

注意

如果指定了子矩阵的数量，则得到的子矩阵相同大小。 这意味着列数必须能被 “parts” 参数整除，没有余数。 也可按子矩阵尺寸数组得到 不同尺寸的子矩阵。 各尺寸数组的元素都可用，直到整个矩阵被分割。 如果数组尺寸分割结束，而矩阵尚有部分未除尽，则未分割的余数将作为最后一个子矩阵。

举例

   matrix matrix_a={{ 1, 2, 3, 4, 5, 6},
                    { 7, 8, 9,10,11,12},
                    {13,14,15,16,17,18}};
   matrix splitted[];
   ulong  parts[]={2,3};
 
   matrix_a.Vsplit(2,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
 
   matrix_a.Vsplit(3,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
 
   matrix_a.Vsplit(parts,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
 
 
  /*
     splitted 0
     [[1,2,3]
      [7,8,9]
      [13,14,15]]
     splitted 1
     [[4,5,6]
      [10,11,12]
      [16,17,18]]
 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4]
      [9,10]
      [15,16]]
     splitted 2
     [[5,6]
      [11,12]
      [17,18]]
 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4,5]
      [9,10,11]
      [15,16,17]]
     splitted 2
     [[6]
      [12]
      [18]]
 
  */

7.3.21 ArgSort

矩阵或向量的间接排序。

vector vector::Sort(
  func_name  compare_func=NULL,  // 比较函数
  T          context             // 自定义排序函数的参数
   );
 
matrix matrix::Sort(
  func_name  compare_func=NULL   // 比较函数
  T          context             // 自定义排序函数的参数
   );
 
matrix matrix::Sort(
  const int  axis,               // 排序轴
  func_name  compare_func=NULL   // 比较函数
  T          context             // 自定义排序函数的参数
   );

参数

axis

[输入] 要排序的轴：0 是水平，1 是垂直。

func_name

[输入] 比较器。 您可以指定 ENUM_SORT_MODE 枚举值之一，或您自己的比较函数。 如果未指定函数，则采用升序排序。

自定义比较函数可以有两种类型：

int comparator(T x1,T x2) int comparator(T x1,T x2,TContext context) 此处 T 是矩阵或向量的类型，而传递给 Sort 方法的附加参数 TContex 则是作为“上下文关联”变量类型。

context

[输入] 可传递给自定义排序函数的其它可选参数。

返回值

含有已排序元素索引的向量或矩阵。 例如，结果 [4,2,0,1,3] 指示元素 4 其索引应该位于零位置，元素 2 其索引位于第一个位置，依此类推。

7.3.22 Sort

就地针对矩阵或向量进行排序。

void vector::Sort(
  func_name  compare_func=NULL,  // 比较函数
  T          context             // 自定义排序函数的参数
   );
 
void matrix::Sort(
  func_name  compare_func=NULL   // 比较函数
  T          context             // 自定义排序函数的参数
   );
 
void matrix::Sort(
  const int  axis,               // 排序轴
  func_name  compare_func=NULL   // 比较函数
  T          context             // 自定义排序函数的参数
   );

参数

axis

[输入] 要排序的轴：0 是水平，1 是垂直。

func_name

[输入] 比较器。 您可以指定 ENUM_SORT_MODE 枚举值之一，或您自己的比较函数。 如果未指定函数，则采用升序排序。

自定义比较函数可以有两种类型：

int comparator(T x1,T x2) int comparator(T x1,T x2,TContext context) 此处 T 是矩阵或向量的类型，而传递给 Sort 方法的附加参数 TContex 则是作为“上下文关联”变量类型。

context

[输入] 可传递给自定义排序函数的其它可选参数。

返回值

无。 排序就地执行，即它应用于调用 Sort 方法的矩阵/向量的数据。

举例

//+------------------------------------------------------------------+
//| Sort 函数                                                         |
//+------------------------------------------------------------------+
int MyDoubleComparator(double x1,double x2,int sort_mode=0)
  {
   int res=x1<x2 ? -1 : (x1>x2 ? 1 : 0);
   return(sort_mode==0 ? res : -res);
  }
//+------------------------------------------------------------------+
//| 脚本程序 start 函数                                                |
//+------------------------------------------------------------------+
void OnStart()
  {
   //--- 填充向量
   vector v(100);
   //--- 升序排序
   v.Sort(MyDoubleComparator);   // 此处使用了默认值为 “0” 的附加参数
   Print(v);
   // 降序排序
   v.Sort(MyDoubleComparator,1); // 此处的附加参数 “1” 是由用户显式指定的
   Print(v);
  }

7.4 矩阵和向量的数学运算

数学运算，包括加法、减法、乘法和除法，可以针对矩阵和向量按元素级执行。

数学函数最初设计用于对标量值执行相关操作。 大多数函数可以应用于矩阵和向量。 其中包括 MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh, 和 MathTanh。 此类操作意味着矩阵和向量的元素级处理。 示例

//---
  matrix a= {{1, 4}, {9, 16}};
  Print("matrix a=\n",a);
  a=MathSqrt(a);
  Print("MatrSqrt(a)=\n",a);
  /*
   matrix a=
   [[1,4]
    [9,16]]
   MatrSqrt(a)=
   [[1,2]
    [3,4]]
  */

对于 MathMod 和 MathPow，第二个元素可以是标量,，或相应大小的矩阵/向量。

下面的示例展示如何将数学函数应用于向量来计算标准偏差。

//+------------------------------------------------------------------+
//| 脚本程序 start 函数                                                |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- 使用初始化函数填充矢量
  vector r(10, ArrayRandom); // 从0 到1 的随机数数组
//--- 计算平均值
  double avr=r.Mean();       // 数组平均值
  vector d=r-avr;            // 计算与平均值的偏差数组
  Print("avr(r)=", avr);
  Print("r=", r);
  Print("d=", d);
  vector s2=MathPow(d, 2);   // 方差平方数组
  double sum=s2.Sum();       // 方差平方和
//--- 以两种不同的方法计算标准偏差
  double std=MathSqrt(sum/r.Size());
  Print(" std(r)=", std);
  Print("r.Std()=", r.Std());   
 }
/*
  avr(r)=0.5300302133243813
  r=[0.8346201971495713,0.8031556138798182,0.6696676534318063,0.05386516922513505,0.5491195410016175,0.8224433118686484,...
  d=[0.30458998382519,0.2731254005554369,0.1396374401074251,-0.4761650440992462,0.01908932767723626,0.2924130985442671, ...
   std(r)=0.2838269732183663
  r.Std()=0.2838269732183663
*/
//+------------------------------------------------------------------+
//| 以随机数值填充向量                                                 |
//+------------------------------------------------------------------+
void ArrayRandom(vector& v)
 {
  for(ulong i=0; i<v.Size(); i++)
    v[i]=double(MathRand())/32767.;
 }

7.4.1 数学运算

数学运算，包括加法、减法、乘法和除法，可以针对矩阵和向量按元素级执行。

两个矩阵或两个向量必须属于同一类型，并且必须具有相同的维度。 矩阵的每个元素都对第二个矩阵的相应元素进行操作。

您还可以使用相应的类型（双精度、浮点数或复数）的标量作为第二项（乘数、减法或除数）。 在这种情况下，矩阵或向量的每个成员都将在指定的标量上运行。

  matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix matrix_b={{1,2,3},{4,5,6}};
 
  matrix matrix_c1=matrix_a+matrix_b;
  matrix matrix_c2=matrix_b-matrix_a;
  matrix matrix_c3=matrix_a*matrix_b;   // 哈达玛（Hadamard）乘积，不要和矩阵乘积混淆！ 对此有一个特殊的 MatMul 函数
  matrix matrix_c4=matrix_b/matrix_a;
 
  matrix_c1=matrix_a+1;
  matrix_c2=matrix_b-double_value;
  matrix_c3=matrix_a*M_PI;
  matrix_c4=matrix_b/0.1;
 
//--- 可以就地采取行动
  matrix_a+=matrix_b;
  matrix_a/=2;

相同的操作可用于向量。

7.4.2 数学函数

以下数学函数可以应用于矩阵和向量：MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh, MathTanh。 此类操作意味着矩阵和向量的元素级处理。

对于 MathMod 和 MathPow，第二个元素既可以是标量，亦或相应大小的矩阵/向量。

   matrix<T> mat1(128,128);
   matrix<T> mat3(mat1.Rows(),mat1.Cols());
   ulong     n,size=mat1.Rows()*mat1.Cols();
...
   mat2=MathPow(mat1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),(T)1.9);
      if(res!=mat2.Flat(n))
         errors++;
     }
   mat2=MathPow(mat1,mat3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),mat3.Flat(n));
      if(res!=mat2.Flat(n))
         errors++;
     }
...
   vector<T> vec1(16384);
   vector<T> vec3(vec1.Size());
   ulong     n,size=vec1.Size();
...
   vec2=MathPow(vec1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],(T)1.9);
      if(res!=vec2[n])
         errors++;
     }
   vec2=MathPow(vec1,vec3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],vec3[n]);
      if(res!=vec2[n])
         errors++;
     }

7.5 乘积

矩阵和矢量乘积 矩阵和向量乘积计算包括：

• 矩阵乘法
• 向量乘法
• 计算协方差矩阵
• 计算两个向量的互相关
• 计算两个向量的卷积
• 计算相关系数

函数	动作
MatMul	两个矩阵的矩阵乘积
GeMM	通用矩阵乘法（GeMM）
Power	将方阵提升整数幂
Dot	两个向量的点积
Kron	返回两个矩阵、矩阵和向量，向量和矩阵、或两个向量的克罗内克（Kronecker）乘积
Inner	两个矩阵的内积
Outer	计算两个矩阵或两个向量的外积
CorrCoef	计算皮尔逊（Pearson）相关系数（线性相关系数）
Cov	计算协方差矩阵
Correlate	计算两个向量的互相关性
Convolve	返回两个向量的离散线性卷积

7.5.1 MatMul

MatMul 方法支持矩阵和向量的乘法，具有若干个重载。

矩阵乘以矩阵: matrix[M][K] * matrix[K][N] = matrix[M][N]

matrix  matrix::MatMul(
  const matrix&  b      // 第二个矩阵
   );

向量乘以矩阵: horizontal vector[K] * matrix[K][N] = horizontal vector[N]

vector  vector::MatMul(
  const matrix&  b      // 矩阵
   );

矩阵乘以向量: matrix[M][K] * vertical vector[K] = vertical vector[M]

vector  matrix::MatMul(
  const vector&  b      // 向量
   );

标量向量乘法: horizontal vector * vertical vector = dot value

scalar  vector::MatMul(
  const vector&  b      // 第二个向量
   );

参数

b

[输入] 矩阵或向量。

返回值

矩阵、矢量或标量，具体取决于所使用的方法。

注意

矩阵应兼容乘法，即第一个矩阵中的列数应等于第二个矩阵中的行数。 矩阵乘法不支持交换律：在一般情况下，将第一个矩阵乘以第二个矩阵的结果不等于将第二个矩阵乘以第一个矩阵的结果。

矩阵积由第一个矩阵的行向量和第二个矩阵的列向量的标量积的所有可能组合组成。

在标量乘法中，向量必须具有相同的长度。

当向量和矩阵相乘时，向量的长度必须与矩阵中的列数完全匹配。

以 MQL5 实现的朴素矩阵乘法算法：

matrix MatrixProduct(const matrix& matrix_a, const matrix& matrix_b)
  {
   matrix matrix_c;
 
   if(matrix_a.Cols()!=matrix_b.Rows())
      return(matrix_c);
      
   ulong M=matrix_a.Rows();
   ulong K=matrix_a.Cols();
   ulong N=matrix_b.Cols();
   matrix_c=matrix::Zeros(M,N);
 
   for(ulong m=0; m<M; m++)
      for(ulong k=0; k<K; k++)
         for(ulong n=0; n<N; n++)
            matrix_c[m][n]+=matrix_a[m][k]*matrix_b[k][n];
 
   return(matrix_c);
  }

矩阵乘法示例

   matrix a={{1, 0, 0},
             {0, 1, 0}};
   matrix b={{4, 1},
             {2, 2},
             {1, 3}};
   matrix c1=a.MatMul(b);
   matrix c2=b.MatMul(a);
   Print("c1 = \n", c1);
   Print("c2 = \n", c2);
/*
   c1 = 
   [[4,1]
    [2,2]]
   c2 = 
   [[4,1,0]
    [2,2,0]
    [1,3,0]]
*/

水平向量乘以矩阵的示例

//+------------------------------------------------------------------+
//| 脚本程序 start 函数                                                |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- 创建一个 3x5 矩阵
   matrix m35;
   m35.Init(3, 5, Arange);
//---
   vector v3 = {1, 2, 3};
   Print("Product of horizontal vector v and matrix m[3,5]");
   Print("On the left, vector v3 = ", v3);
   Print("On the right, matrix m35 = \n", m35);
   Print("v3.MatMul(m35) = horizontal vector v[5] \n", v3.MatMul(m35));
 
  /* 结果
    Product of horizontal vector v3 and matrix m[3,5]
    On the left, vector v3 = [1,2,3]
    On the right, matrix m35 =
    [[0,1,2,3,4]
     [5,6,7,8,9]
     [10,11,12,13,14]]
    v3.MatMul(m35) = horizontal vector v[5]
    [40,46,52,58,64]
   */
  }
//+------------------------------------------------------------------+
//|  以递增数值填充矩阵                                                |
//+------------------------------------------------------------------+
void Arange(matrix & m, double start = 0, double step = 1)
  {
//---
   ulong cols = m.Cols();
   ulong rows = m.Rows();
   double value = start;
   for(ulong r = 0; r < rows; r++)
     {
      for(ulong c = 0; c < cols; c++)
        {
         m[r][c] = value;
         value += step;
        }
     }
//---
  }

矩阵如何乘以垂直向量的示例

//+------------------------------------------------------------------+
//| 脚本程序 start 函数                                                |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- 创建一个 3x5 矩阵
   matrix m35;
   m35.Init(3, 5, Arange);
//---
   Print("Product of matrix m[3,5] and vertical vector v[5]");
   vector v5 = {1,2,3,4,5};
   Print("On the left, m35 = \n",m35);
   Print("On the right v5 = ",v5);
   Print("m35.MatMul(v5) = vertical vector v[3] \n",m35.MatMul(v5));
 
  /* 结果
   Product of matrix m[3,5] and vertical vector v[5]
   On the left, m35 = 
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   On the right, v5 = [1,2,3,4,5]
   m35.MatMul(v5) = vertical vector v[3] 
   [40,115,190]

参见

Dot, GeMM

7.5.2 GeMM

GeMM（通用矩阵乘法）方法实现了两个矩阵的一般乘法。 运算定义为 C ← α A B + β C，其中 A 和 B 矩阵可以选择转置。 配合矩阵 AB（MatMul）的正态乘法，假定 alpha 标量等于 1，beta 等于零。

GeMM 和 MatMul 在效率方面的主要区别在于，MatMul 总是创建一个新的矩阵/矢量对象，而 GeMM 使用现有的矩阵对象，且不会重新创建它。 因此，当您使用 GeMM 并为相应的矩阵预分配内存时，在操控相同的矩阵大小时，将不会重新分配内存。 这可能是 GeMM 在批量计算方面的一个重要优势，例如，在策略测试器中运行优化、或训练神经网络时。

与 MatMul 类似，GeMM 也有 4 个重载。 然而，第四次重载的语义已被修改，以便能够将垂直向量与水平向量相乘。

在现有的矩阵/矢量对象中，没有必要预先分配内存。 将在第一次调用 GeMM 时分配内存，并以零填充。

矩阵乘以矩阵: matrix C[M][N] = α * ( matrix A[M][K] * matrix B[K][N]) + β * matrix C[M][N]

bool  matrix::GeMM(
  const matrix &A,    // first matrix
  const matrix &B,    // second matrix
  double alpha,       // 乘积 AB 的 alpha 乘数
  double beta,        // beta multiplier for matrix C
  uint   flags        // a combination of ENUM_GEMM values (bitwise OR), which determines whether matrices A, B and C are transposed
   );

向量乘以矩阵: vector C[N] = α * ( vector A[K] * matrix B[K][N]) + β * vector C[N]

bool  vector::GeMM(
  const vector &A,    // 水平向量
  const matrix &B,    // 矩阵
  double alpha,       // 乘积 AB 的 alpha 乘数
  double beta,        // 向量 C 的 beta 乘数
  uint   flags        // ENUM_GEMM 枚举值，判定是否矩阵 A 是转置
   );

矩阵乘以向量: vector C[M] = α * ( matrix A[M][K] * vector B[K] * ) + β * vector C[M]

bool  vector::GeMM(
  const matrix &A,    // 矩阵
  const vector &B,    // 垂直向量
  double alpha,       // 乘积 AB 的 alpha 乘数
  double beta,        // 向量 C 的 beta 乘数
  uint   flags        // ENUM_GEMM 枚举值，判定是否矩阵 B 是转置
   );

向量乘以向量: matrix C[M][N] = α * ( vector A[M] * vector B[N] * ) + β * matrix C[M][N]. 此重载返回一个矩阵，与 MatMul 不同，它返回一个标量。

bool  matrix::GeMM(
  const vector &A,    // 第一个向量
  const vector &B,    // 第二个向量
  double alpha,       // 乘积 AB 的 alpha 乘数
  double beta,        // 用于矩阵 C 的 beta
  uint   flags        // ENUM_GEMM 枚举值，判定是否矩阵 C 是转置
   );

参数

A

[输入] 矩阵或向量。

B

[输入] 矩阵或向量。

alpha

[输入] AB 乘积的阿尔法乘数。

beta

[输入] 所得 C 矩阵的贝塔乘数。

flags

[输入] 确定是否转置矩阵 A、B 和 C 的 ENUM_GEMM 枚举值。

返回值

成功返回 true，否则 false。

ENUM_GEMM

GeMM 方法的标志枚举。 |ID|说明| |TRANSP_A|使用转置矩阵 A| |TRANSP_B|使用转置矩阵 B| |TRANSP_C|使用转置矩阵 C|

注意

浮点型、双精度型和复数类型的矩阵和向量可以用作参数 A 和 B。GeMM 方法的模板变体如下：

bool matrix<T>::GeMM(const matrix<T> &A,const matrix<T> &B,T alpha,T beta,ulong flags);
bool matrix<T>::GeMM(const vector<T> &A,const vector<T> &B,T alpha,T beta,ulong flags);
 
bool vector<T>::GeMM(const vector<T> &A,const matrix<T> &B,T alpha,T beta,ulong flags);
bool vector<T>::GeMM(const matrix<T> &A,const vector<T> &B,T alpha,T beta,ulong flags);

基本上一般的矩阵乘法函数描述为：

C[m,n] = α *Sum(A[m,k]*B[k,n]) + β*C[m,n]

配合以下尺寸：矩阵 A 为 M x K，矩阵 B 为 K x N，矩阵 C 为 M x N。

因此，矩阵应该与乘法兼容，即第一个矩阵中的列数应等于第二个矩阵中的行数。 矩阵乘法不支持交换律：在一般情况下，将第一个矩阵乘以第二个矩阵的结果不等于将第二个矩阵乘以第一个矩阵的结果。

示例:

void OnStart()
  {
   vector vector_a= {1, 2, 3, 4, 5};
   vector vector_b= {4, 3, 2, 1};
   matrix matrix_c;
//--- 计算两个向量的 GeMM
   matrix_c.GeMM(vector_a, vector_b, 1, 0);
   Print("matrix_c:\n ", matrix_c, "\n");
   /*
   matrix_c:
    [[4,3,2,1]
    [8,6,4,2]
    [12,9,6,3]
    [16,12,8,4]
    [20,15,10,5]]
   */
//--- 创建矩阵作为向量
   matrix matrix_a(5, 1);
   matrix matrix_b(1, 4);
   matrix_a.Col(vector_a, 0);
   matrix_b.Row(vector_b, 0);
   Print("matrix_a:\n ", matrix_a);
   Print("matrix_b:\n ", matrix_b);
   /*
   matrix_a:
   [[1]
   [2]
   [3]
   [4]
   [5]]
   matrix_b:
   [[4,3,2,1]]
   */
//-- 计算两个矩阵的 GeMM 并获取相同的结果
   matrix_c.GeMM(matrix_a, matrix_b, 1, 0);
   Print("matrix_c:\n ", matrix_c);
   /*
   matrix_c:
    [[4,3,2,1]
    [8,6,4,2]
    [12,9,6,3]
    [16,12,8,4]
    [20,15,10,5]]
   */
  }

参见

MatMul

7.5.3 Power

将方阵提升整数幂。

matrix matrix::Power(
  const int  power      // 幂
   );

参数

power

[输入] 指数可以是任何整数、正数、负数或零。

返回值

矩阵。

注意

生成的矩阵与原始矩阵的大小相同。 当升幂为 0 时，返回单位矩阵。 正幂 n 表示原始矩阵自身乘以 n 次。 负幂 -n 表示原始矩阵先倒置，然后将倒置矩阵乘以自身 n 次。

以 MQL5 实现的矩阵升幂的简单算法：

bool MatrixPower(matrix& c, const matrix& a, const int power)
  {
//--- 矩阵必须是正阵
   if(a.Rows()!=a.Cols())
      return(false);
//--- 结果矩阵的大小完全相同
   ulong  rows=a.Rows();
   ulong  cols=a.Cols();
   matrix result(rows,cols);
//--- 当幂为零时，返回单位矩阵
   if(power==0)
      result.Identity();
   else
     {
      //--- 对于负值，首先反转矩阵
      if(power<0)
        {
         matrix inverted=a.Inv();
         result=inverted;
         for(int i=-1; i>power; i--)
            result=result.MatMul(inverted);
        }
      else
        {
         result=a;
         for(int i=1; i<power; i++)
            result=result.MatMul(a);
        }
     }
//---
   c=result;
   return(true);
  }

MQL5 示例:

  matrix i= {{0, 1}, {-1, 0}};
  Print("i:\n", i);
 
  Print("i.Power(3):\n", i.Power(3));
 
  Print("i.Power(0):\n", i.Power(0));
 
  Print("i.Power(-3):\n", i.Power(-3));
 
  /*
  i:
  [[0,1]
   [-1,0]]
 
  i.Power(3):
  [[0,-1]
   [1,0]]
 
  i.Power(0):
  [[1,0]
   [0,1]]
 
  i.Power(-3):
  [[0, -1]
   [1,0]]
  */

Python 示例:

import numpy as np
from numpy.linalg import matrix_power
 
# matrix equiv. of the imaginary unit
i = np.array([[0, 1], [-1, 0]]) 
print("i:\n",i)
 
# should = -i
print("matrix_power(i, 3) :\n",matrix_power(i, 3) )
 
print("matrix_power(i, 0):\n",matrix_power(i, 0))
 
# should = 1/(-i) = i, but w/ f.p. elements
print("matrix_power(i, -3):\n",matrix_power(i, -3))
 
i:
 [[ 0  1]
 [-1  0]]
 
matrix_power(i, 3) :
 [[ 0 -1]
 [ 1  0]]
 
matrix_power(i, 0):
 [[1 0]
 [0 1]]
 
matrix_power(i, -3):
 [[ 0.  1.]
 [-1.  0.]]

7.5.4 Dot

两个向量的点积。

double vector::Dot(
  const vector&  b      // 第二个向量
   );

参数

b

[输入] 向量。

返回值

标量。

注意

两个矩阵的点积是矩阵乘积 matrix::MatMul()。

以 MQL5 实现的向量标量乘积的简单算法：

double VectorDot(const vector& vector_a, const vector& vector_b)
  {
   double dot=0;
 
   if(vector_a.Size()==vector_b.Size())
     {
      for(ulong i=0; i<vector_a.Size(); i++)
         dot+=vector_a[i]*vector_b[i];
     }
 
   return(dot);
  }

MQL5 示例:

   for(ulong i=0; i<rows; i++)
     {
      vector v1=a.Row(i);
      for(ulong j=0; j<cols; j++)
        {
         vector v2=b.Row(j);
         result[i][j]=v1.Dot(v2);
        }
     }

Python 示例:

import numpy as np
 
a = [1, 0, 0, 1]
b = [4, 1, 2, 2]
print(np.dot(a, b))
 
>>> 6

7.5.5 Kron

返回两个矩阵的克罗内克（Kronecker）乘积，矩阵和向量，向量和矩阵、或两个向量。

matrix matrix::Kron(
  const matrix&  b      // 第二个矩阵
   );
 
matrix matrix::Kron(
  const vector&  b      // 向量
   );
 
matrix vector::Kron(
  const matrix&  b      // 矩阵
   );
 
matrix vector::Kron(
  const vector&  b      // 第二个向量
   );

参数

b

[输入] 第二个矩阵。

返回值

矩阵。

注意

克罗内克（Kronecker）乘积也称为块矩阵乘法。

以 MQL5 实现的两个矩阵克罗内克（Kronecker）乘积的简单算法：

matrix MatrixKronecker(const matrix& matrix_a,const matrix& matrix_b)
  {
   ulong  M=matrix_a.Rows();
   ulong  N=matrix_a.Cols();
   ulong  P=matrix_b.Rows();
   ulong  Q=matrix_b.Cols();
   matrix matrix_c(M*P,N*Q);
 
   for(ulong m=0; m<M; m++)
      for(ulong n=0; n<N; n++)
         for(ulong p=0; p<P; p++)
            for(ulong q=0; q<Q; q++)
               matrix_c[m*P+p][n*Q+q]=matrix_a[m][n] * matrix_b[p][q];
 
   return(matrix_c);
  }

MQL5 示例:

   matrix a={{1,2,3},{4,5,6}};
   matrix b=matrix::Identity(2,2);
   vector v={1,2};
 
   Print(a.Kron(b));
   Print(a.Kron(v));
 
  /*
   [[1,0,2,0,3,0]
    [0,1,0,2,0,3]
    [4,0,5,0,6,0]
    [0,4,0,5,0,6]]
 
   [[1,2,2,4,3,6]
    [4,8,5,10,6,12]]
  */

Python 示例:

import numpy as np
 
A = np.arange(1,7).reshape(2,3)
B = np.identity(2)
V = [1,2]
print(np.kron(A, B))
print("")
print(np.kron(A, V))
 
[[1. 0. 2. 0. 3. 0.]
 [0. 1. 0. 2. 0. 3.]
 [4. 0. 5. 0. 6. 0.]
 [0. 4. 0. 5. 0. 6.]]
 
[[ 1  2  2  4  3  6]
 [ 4  8  5 10  6 12]]

7.5.6 Inner

两个矩阵的内积。

matrix matrix::Inner(
  const matrix&  b      // 第二个矩阵
   );

参数

b

[输入] 矩阵。

返回值

矩阵。

注意

两个向量的内积是两个向量的点积 vector::Dot()。

以 MQL5 实现的两个矩阵内积的简单算法：

bool MatrixInner(matrix& c, const matrix& a, const matrix& b)
  {
//--- 列数必须相等
   if(a.Cols()!=b.Cols())
      return(false);
//--- 所得矩阵的大小取决于每个矩阵中向量的数量
   ulong  rows=a.Rows();
   ulong  cols=b.Rows();
   matrix result(rows,cols);
//---
   for(ulong i=0; i<rows; i++)
     {
      vector v1=a.Row(i);
      for(ulong j=0; j<cols; j++)
        {
         vector v2=b.Row(j);
         result[i][j]=v1.Dot(v2);
        }
     }
//---
   c=result;
   return(true);
  }

MQL5 示例:

   matrix a={{0,1,2},{3,4,5}};
   matrix b={{0,1,2},{3,4,5},{6,7,8}};
   matrix c=a.Inner(b);
   Print(c);
   matrix a1={{0,1,2}};
   matrix c1=a1.Inner(b);
   Print(c1);
 
  /*
  [[5,14,23]
  [14,50,86]]
  [[5,14,23]]
  */

Python 示例:

import numpy as np
 
A = np.arange(6).reshape(2, 3)
B = np.arange(9).reshape(3, 3)
A1= np.arange(3)
print(np.inner(A, B))
print("");
print(np.inner(A1, B))

7.5.7 Outer

计算两个矩阵或两个向量的外积。

matrix matrix::Outer(
  const matrix&  b      // 第二个矩阵
   );
 
matrix vector::Outer(
  const vector&  b      // 第二个向量
   );

参数

b

[输入] 矩阵。

返回值

矩阵。

注意

外积，如克罗内克（Kronecker）乘积，也是一个区块矩阵（和向量）乘法。

以 MQL5 实现的两个矩阵外积的简单算法：

matrix MatrixOuter(const matrix& matrix_a, const matrix& matrix_b)
  {
//--- 生成的矩阵大小取决于矩阵的大小
   ulong  rows=matrix_a.Rows()*matrix_a.Cols();
   ulong  cols=matrix_b.Rows()*matrix_b.Cols();
   matrix matrix_c(rows,cols);
   ulong  cols_a=matrix_a.Cols();
   ulong  cols_b=matrix_b.Cols();
//---
   for(ulong i=0; i<rows; i++)
     {
      ulong row_a=i/cols_a;
      ulong col_a=i%cols_a;
      for(ulong j=0; j<cols; j++)
        {
         ulong row_b=j/cols_b;
         ulong col_b=j%cols_b;
         matrix_c[i][j]=matrix_a[row_a][col_a] * matrix_b[row_b][col_b];
        }
     }
//---
   return(matrix_c);
  }

MQL5 示例:

   vector vector_a={0,1,2,3,4,5};
   vector vector_b={0,1,2,3,4,5,6};
   Print("vector_a.Outer\n",vector_a.Outer(vector_b));
   Print("vector_a.Kron\n",vector_a.Kron(vector_b));
 
   matrix matrix_a={{0,1,2},{3,4,5}};
   matrix matrix_b={{0,1,2},{3,4,5},{6,7,8}};
   Print("matrix_a.Outer\n",matrix_a.Outer(matrix_b));
   Print("matrix_a.Kron\n",matrix_a.Kron(matrix_b));
 
  /*
   vector_a.Outer
   [[0,0,0,0,0,0,0]
    [0,1,2,3,4,5,6]
    [0,2,4,6,8,10,12]
    [0,3,6,9,12,15,18]
    [0,4,8,12,16,20,24]
    [0,5,10,15,20,25,30]]
   vector_a.Kron
   [[0,0,0,0,0,0,0,0,1,2,3,4,5,6,0,2,4,6,8,10,12,0,3,6,9,12,15,18,0,4,8,12,16,20,24,0,5,10,15,20,25,30]]
   matrix_a.Outer
   [[0,0,0,0,0,0,0,0,0]
    [0,1,2,3,4,5,6,7,8]
    [0,2,4,6,8,10,12,14,16]
    [0,3,6,9,12,15,18,21,24]
    [0,4,8,12,16,20,24,28,32]
    [0,5,10,15,20,25,30,35,40]]
   matrix_a.Kron
   [[0,0,0,0,1,2,0,2,4]
    [0,0,0,3,4,5,6,8,10]
    [0,0,0,6,7,8,12,14,16]
    [0,3,6,0,4,8,0,5,10]
    [9,12,15,12,16,20,15,20,25]
    [18,21,24,24,28,32,30,35,40]]
   */

Python 示例:

import numpy as np
 
A = np.arange(6)
B = np.arange(7)
print("np.outer")
print(np.outer(A, B))
print("np.kron")
print(np.kron(A, B))
 
A = np.arange(6).reshape(2, 3)
B = np.arange(9).reshape(3, 3)
print("np.outer")
print(np.outer(A, B))
print("np.kron")
 
np.outer
[[ 0  0  0  0  0  0  0]
 [ 0  1  2  3  4  5  6]
 [ 0  2  4  6  8 10 12]
 [ 0  3  6  9 12 15 18]
 [ 0  4  8 12 16 20 24]
 [ 0  5 10 15 20 25 30]]
np.kron
[ 0  0  0  0  0  0  0  0  1  2  3  4  5  6  0  2  4  6  8 10 12  0  3  6
  9 12 15 18  0  4  8 12 16 20 24  0  5 10 15 20 25 30]
np.outer
[[ 0  0  0  0  0  0  0  0  0]
 [ 0  1  2  3  4  5  6  7  8]
 [ 0  2  4  6  8 10 12 14 16]
 [ 0  3  6  9 12 15 18 21 24]
 [ 0  4  8 12 16 20 24 28 32]
 [ 0  5 10 15 20 25 30 35 40]]
np.kron
[[ 0  0  0  0  1  2  0  2  4]
 [ 0  0  0  3  4  5  6  8 10]
 [ 0  0  0  6  7  8 12 14 16]
 [ 0  3  6  0  4  8  0  5 10]
 [ 9 12 15 12 16 20 15 20 25]
 [18 21 24 24 28 32 30 35 40]]

7.5.8 CorrCoef

计算皮尔逊（Pearson）相关系数（线性相关系数）。

matrix matrix::CorrCoef(
  const bool    rowvar=true  // 所观测向量的行或列
);
 
scalar vector::CorrCoef(
  const vector&  b           // 第二个向量
);

返回值

皮尔逊（Pearson）乘积矩相关系数。

注意

相关系数在 [-1, 1] 范围内。

由于浮点舍入，生成的数组可能不是埃尔米特（Hermitian）数组，对角元素也许不是 1，并且元素也许不满足不等式 abs(a) <= 1。 实部和虚部被剪裁到区间 [-1, 1]，以便试图改善这种情况，但在复杂情况下并无多大帮助。

以 MQL5 实现的计算两个向量相关系数的简单算法：

double VectorCorrelation(const vector& vector_x,const vector& vector_y)
  {
   ulong n=vector_x.Size()<vector_y.Size() ? vector_x.Size() : vector_y.Size();
   if(n<=1)
      return(0);
 
   ulong  i;
   double xmean=0;
   double ymean=0;
   for(i=0; i<n; i++)
     {
      if(!MathIsValidNumber(vector_x[i]))
         return(0);
      if(!MathIsValidNumber(vector_y[i]))
         return(0);
      xmean+=vector_x[i];
      ymean+=vector_y[i];
     }
   xmean/=(double)n;
   ymean/=(double)n;
 
   double s=0;
   double xv=0;
   double yv=0;
   double t1=0;
   double t2=0;
//--- 计算
   s=0;
   for(i=0; i<n; i++)
     {
      t1=vector_x[i]-xmean;
      t2=vector_y[i]-ymean;
      xv+=t1*t1;
      yv+=t2*t2;
      s+=t1*t2;
     }
//--- 检查
   if(xv==0 || yv==0)
      return(0);
//--- 返回结果
   return(s/(MathSqrt(xv)*MathSqrt(yv)));
  }

MQL5 示例:

   vectorf vector_a={1,2,3,4,5};
   vectorf vector_b={0,1,0.5,2,2.5};
   Print("vectors correlation ",vector_a.CorrCoef(vector_b));
//---
   matrixf matrix_a={{1,2,3,4,5},
                    {0,1,0.5,2,2.5}};
   Print("matrix rows correlation\n",matrix_a.CorrCoef());
   matrixf matrix_a2=matrix_a.Transpose();
   Print("transposed matrix cols correlation\n",matrix_a2.CorrCoef(false));
   matrixf matrix_a3={{1.0f, 2.0f, 3.0f, 4.0f, 5.0f},
                      {0.0f, 1.0f, 0.5f, 2.0f, 2.5f},
                      {0.1f, 1.0f, 2.0f, 1.0f, 0.3f}};
   Print("rows correlation\n",matrix_a3.CorrCoef());
   Print("cols correlation\n",matrix_a3.CorrCoef(false));
 
  /*
   vectors correlation 0.9149913787841797
   matrix rows correlation
   [[1,0.91499138]
    [0.91499138,1]]
   transposed matrix cols correlation
   [[1,0.91499138]
    [0.91499138,1]]
   rows correlation
   [[1,0.91499138,0.08474271]
    [0.91499138,1,-0.17123166]
    [0.08474271,-0.17123166,1]]
   cols correlation
   [[1,0.99587059,0.85375023,0.91129309,0.83773589]
    [0.99587059,1,0.80295509,0.94491106,0.88385159]
    [0.85375023,0.80295509,1,0.56362146,0.43088508]
    [0.91129309,0.94491106,0.56362146,1,0.98827404]
    [0.83773589,0.88385159,0.43088508,0.98827404,1]]
   */

Python 示例:

import numpy as np
va=[1,2,3,4,5]
vb=[0,1,0.5,2,2.5]
print("vectors correlation")
print(np.corrcoef(va,vb))
 
ma=np.zeros((2,5))
ma[0,:]=va
ma[1,:]=vb
print("matrix rows correlation")
print(np.corrcoef(ma))
print("transposed matrix cols correlation")
print(np.corrcoef(np.transpose(ma),rowvar=False))
print("")
 
ma1=[[1,2,3,4,5],[0,1,0.5,2,2.5],[0.1,1,0.2,1,0.3]]
print("rows correlation\n",np.corrcoef(ma1))
print("cols correlation\n",np.corrcoef(ma1,rowvar=False))
 
transposed matrix cols correlation
[[1.         0.91499142]
 [0.91499142 1.        ]]
 
rows correlation
 [[1.         0.91499142 0.1424941 ]
 [0.91499142 1.         0.39657517]
 [0.1424941  0.39657517 1.        ]]
cols correlation
 [[1.         0.99587059 0.98226063 0.91129318 0.83773586]
 [0.99587059 1.         0.99522839 0.94491118 0.88385151]
 [0.98226063 0.99522839 1.         0.97234063 0.92527551]
 [0.91129318 0.94491118 0.97234063 1.         0.98827406]
 [0.83773586 0.88385151 0.92527551 0.98827406 1.        ]]

7.5.9 Cov

计算协方差矩阵。

matrix matrix::Cov(
  const bool    rowvar=true  // 所观测向量的行或列
);
 
matrix vector::Cov(
  const vector&  b           // 第二个向量
);

参数

b

[输入] 第二个向量。

注意

计算协方差矩阵。

以 MQL5 实现的计算两个向量的协方差矩阵的简单算法：

bool VectorCovariation(const vector& vector_a,const vector& vector_b,matrix& matrix_c)
  {
   int i,j;
   int m=2;
   int n=(int)(vector_a.Size()<vector_b.Size()?vector_a.Size():vector_b.Size());
//--- 检查
   if(n<=1)
      return(false);
   for(i=0; i<n; i++)
     {
      if(!MathIsValidNumber(vector_a[i]))
         return(false);
      if(!MathIsValidNumber(vector_b[i]))
         return(false);
     }
//---
   matrix matrix_x(2,n);
   matrix_x.Row(vector_a,0);
   matrix_x.Row(vector_b,1);
   vector t=vector::Zeros(m);
//--- 计算
   for(i=0; i<m; i++)
      for(j=0; j<n; j++)
         t[i]+=matrix_x[i][j]/double(n);
   for(i=0; i<m; i++)
      for(j=0; j<n; j++)
         matrix_x[i][j]-=t[i];
//--- syrk C=alpha*A^H*A+beta*C (beta=0 且不考虑)
   matrix_c=matrix::Zeros(m,m);
   for(i=0; i<m; i++)
     {
      for(j=0; j<n; j++)
        {
         double v=matrix_x[i][j]/(n-1);
         for(int i_=i; i_<m; i_++)
            matrix_c[i][i_]+=v*matrix_x[i_][j];
        }
     }
//--- 强制对称性
   for(i=0; i<m-1; i++)
      for(j=i+1; j<m; j++)
         matrix_c[j][i]=matrix_c[i][j];
//---
   return(true);
  }

MQL5 示例:

   matrix matrix_a={{3,-2.1},{1.1,-1},{0.12,4.3}};
   Print("covariation cols\n",matrix_a.Cov(false));
   Print("covariation rows\n",matrix_a.Cov());
   
   vector vector_a=matrix_a.Col(0);
   vector vector_b=matrix_a.Col(1);
   Print("covariation vectors\n",vector_a.Cov(vector_b));
 
  /*
   covariation cols
   [[2.144133333333333,-4.286]
    [-4.286,11.71]]
   covariation rows
   [[13.005,5.355,-10.659]
    [5.355,2.205,-4.389]
    [-10.659,-4.389,8.736199999999998]]
   covariation vectors
   [[2.144133333333333,-4.286]
    [-4.286,11.71]]
  */

Python 示例:

import numpy as np
matrix_a=np.array([[3,-2.1],[1.1,-1],[0.12,4.3]])
matrix_c=np.cov(matrix_a,rowvar=False)
print("covariation cols\n",matrix_c)
matrix_c2=np.cov(matrix_a)
print("covariation rows\n",matrix_c2)
 
vector_a=matrix_a[:,0]
vector_b=matrix_a[:,1]
matrix_c3=np.cov(vector_a,vector_b)
print("covariation vectors\n",matrix_c3)
 
covariation cols
 [[ 2.14413333 -4.286     ]
 [-4.286      11.71      ]]
covariation rows
 [[ 13.005    5.355  -10.659 ]
 [  5.355    2.205   -4.389 ]
 [-10.659   -4.389    8.7362]]
covariation vectors
 [[ 2.14413333 -4.286     ]
 [-4.286      11.71      ]]

7.5.10 Correlate

计算两个向量的互相关。

vector vector::Correlate(
  const vector&          v,        // 向量
  ENUM_VECTOR_CONVOLVE   mode      // 模式
   );

参数

v

[输入] 第二个向量。

mode

[输入] “mode” 参数判定线性卷积计算模式。 数值来自 ENUM_VECTOR_CONVOLVE 枚举。

返回值

两个向量的互相关。

注意

“mode” 参数判定线性卷积计算模式。

以 MQL5 实现的计算两个向量相关系数的简单算法：

vector VectorCrossCorrelationFull(const vector& a,const vector& b)
  {
   int    m=(int)a.Size();
   int    n=(int)b.Size();
   int    size=m+n-1;
   vector c=vector::Zeros(size);
 
   for(int i=0; i<n; i++)
      for(int i_=i; i_<i+m; i_++)
         c[i_]+=b[n-i-1]*a[i_-i];
 
   return(c);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector VectorCrossCorrelationSame(const vector& a,const vector& b)
  {
   int    m=(int)a.Size();
   int    n=(int)b.Size();
   int    size=MathMax(m,n);
   vector c=vector::Zeros(size);
 
   for(int i=0; i<n; i++)
     {
      for(int i_=i; i_<i+m; i_++)
        {
         int k=i_-size/2+1;
         if(k>=0 && k<size)
            c[k]+=b[n-i-1]*a[i_-i];
        }
     }
 
   return(c);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector VectorCrossCorrelationValid(const vector& a,const vector& b)
  {
   int    m=(int)a.Size();
   int    n=(int)b.Size();
   int    size=MathMax(m,n)-MathMin(m,n)+1;
   vector c=vector::Zeros(size);
 
   for(int i=0; i<n; i++)
     {
      for(int i_=i; i_<i+m; i_++)
        {
         int k=i_-n+1;
         if(k>=0 && k<size)
            c[k]+=b[n-i-1]*a[i_-i];
        }
     }
 
   return(c);
  }

MQL5 示例:

   vector a={1,2,3,4,5};
   vector b={0,1,0.5};
 
   Print("full\n",a.Correlate(b,VECTOR_CONVOLVE_FULL));
   Print("same\n",a.Correlate(b,VECTOR_CONVOLVE_SAME));
   Print("valid\n",a.Correlate(b,VECTOR_CONVOLVE_VALID));
   Print("full\n",b.Correlate(a,VECTOR_CONVOLVE_FULL));
 
  /*
   full
   [0.5,2,3.5,5,6.5,5,0]
   same
   [2,3.5,5,6.5,5]
   valid
   [3.5,5,6.5]
   full
   [0,5,6.5,5,3.5,2,0.5]
  */

Python 示例:

import numpy as np
a=[1,2,3,4,5]
b=[0,1,0.5]
 
print("full\n",np.correlate(a,b,'full'))
print("same\n",np.correlate(a,b,'same'));
print("valid\n",np.correlate(a,b,'valid'));
print("full\n",np.correlate(b,a,'full'))
 
full
 [0.5 2.  3.5 5.  6.5 5.  0. ]
same
 [2.  3.5 5.  6.5 5. ]
valid
 [3.5 5.  6.5]
full
 [0.  5.  6.5 5.  3.5 2.  0.5]

7.5.11 Convolve

返回两个向量的离散线性卷积

vector vector::Convolve(
  const vector&           v,        // 向量
  ENUM_VECTOR_CONVOLVE    mode      // 模式
   );

参数

v

[输出] 第二个向量。

mode

[输入] “mode” 参数判定线性卷积计算模式 ENUM_VECTOR_CONVOLVE。

返回值

两个向量的离散，线性卷积。

以 MQL5 实现的计算两个向量卷积的简单算法：

vector VectorConvolutionFull(const vector& a,const vector& b)
  {
   if(a.Size()<b.Size())
      return(VectorConvolutionFull(b,a));
 
   int    m=(int)a.Size();
   int    n=(int)b.Size();
   int    size=m+n-1;
   vector c=vector::Zeros(size);
 
   for(int i=0; i<n; i++)
      for(int i_=i; i_<i+m; i_++)
         c[i_]+=b[i]*a[i_-i];
 
   return(c);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector VectorConvolutionSame(const vector& a,const vector& b)
  {
   if(a.Size()<b.Size())
      return(VectorConvolutionSame(b,a));
 
   int    m=(int)a.Size();
   int    n=(int)b.Size();
   int    size=MathMax(m,n);
   vector c=vector::Zeros(size);
 
   for(int i=0; i<n; i++)
     {
      for(int i_=i; i_<i+m; i_++)
        {
         int k=i_-size/2+1;
         if(k>=0 && k<size)
            c[k]+=b[i]*a[i_-i];
        }
     }
 
   return(c);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector VectorConvolutionValid(const vector& a,const vector& b)
  {
   if(a.Size()<b.Size())
      return(VectorConvolutionValid(b,a));
 
   int    m=(int)a.Size();
   int    n=(int)b.Size();
   int    size=MathMax(m,n)-MathMin(m,n)+1;
   vector c=vector::Zeros(size);
 
   for(int i=0; i<n; i++)
     {
      for(int i_=i; i_<i+m; i_++)
        {
         int k=i_-n+1;
         if(k>=0 && k<size)
            c[k]+=b[i]*a[i_-i];
        }
     }
 
   return(c);
  }

MQL5 示例:

  vector a= {1, 2, 3, 4, 5};
  vector b= {0, 1, 0.5};
 
  Print("full\n", a.Convolve(b, VECTOR_CONVOLVE_FULL));
  Print("same\n", a.Convolve(b, VECTOR_CONVOLVE_SAME));
  Print("valid\n", a.Convolve(b, VECTOR_CONVOLVE_VALID));
 
  /*
   full
   [0,1,2.5,4,5.5,7,2.5]
   same
   [1,2.5,4,5.5,7]
   valid
   [2.5,4,5.5]
  */

Python 示例:

import numpy as np
a=[1,2,3,4,5]
b=[0,1,0.5]
 
print("full\n",np.convolve(a,b,'full'))
print("same\n",np.convolve(a,b,'same'));
print("valid\n",np.convolve(a,b,'valid'));
 
 
full
 [0.  1.  2.5 4.  5.5 7.  2.5]
same
 [1.  2.5 4.  5.5 7. ]
valid
 [2.5 4.  5.5]

7.6 矩阵变换

矩阵分解可用于以下情况：

• 作为求解线性方程组的中间步骤
• 用于矩阵反演
• 计算行列式时
• 查找矩阵的本征值和本征向量时
• 计算矩阵的解析函数时
• 使用最小二乘法时
• 在微分方程的数值解中

根据问题采用不同的矩阵分解类型。

函数	动作
Cholesky	计算乔列斯基分解
Eig	计算方阵的本征值和右本征向量
EigVals	计算一般矩阵的本征值
LU	矩阵的 LU 因数分解为下三角矩阵和上三角矩阵的乘积
LUP	具有部分枢轴的 LUP 因数分解，仅指具有行排列的 LU 分解：PA=LU
QR	计算矩阵的 QR 分解
SVD	奇异值分解

7.6.1 Cholesky

计算乔列斯基（Cholesky）分解。

bool matrix::Cholesky(
  matrix&  L      // 矩阵
   );

参数

L 键

[输出] 下三角矩阵。

返回值

成功时返回 true，否则返回 false。

注意

返回方阵 a 的乔列斯基分解，L * L.H，其中 L 是下三角形和，且 H 是共轭转置运算符（如果 a 是实值，则为普通转置）。 a 必须是埃尔米特（Hermitian，如果实值是对称的），且正定。 不执行任何检查来验证 a 是否是埃尔米特（Hermitian）。 此外，仅用到 a 的下三角形和对角线元素。 仅有 L 实际返回。

举例

  matrix matrix_a= {{5.7998084, -2.1825367}, {-2.1825367, 9.85910595}};
  matrix matrix_l;
  Print("matrix_a\n", matrix_a);
 
  matrix_a.Cholesky(matrix_l);
  Print("matrix_l\n", matrix_l);
  Print("check\n", matrix_l.MatMul(matrix_l.Transpose()));
  
  /*
  matrix_a
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  matrix_l
  [[2.408279136645086,0]
   [-0.9062640068544704,3.006291985133859]]
  check
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  */

7.6.2 Eig

计算方阵的本征值和右本征向量。

bool matrix::Eig(
  matrix&  eigen_vectors,         // 本征向量矩阵
  vector&  eigen_values           // 本征向量向量
   );

特征值和特征向量的复解

bool matrix::Eig(
  matrix<complex>& eigen_vectors, // 特征向量矩阵
  vector<complex>& eigen_values   // 特征值向量
   );

参数

eigen_vectors

[输出] 垂直本征向量矩阵。

eigen_values

[输出] 本征值向量。

返回值

成功时返回 true，否则返回 false。

注意

如果计算特征值时遇到复解，则停止计算，并将错误代码设置为4019 (ERR_MATH_OVERFLOW)。使用Eig方法的复数重载在复数空间中获得完整的解决方案

如果一个复特征值的虚部等于零，那么它就是一个实特征值。这可以在下面的示例中看到。

示例：

void OnStart()
  {
   matrix matrix_a =
     {
        {-3.474589, 1.106384, -9.091977,-3.925227 },
        {-5.522139, 2.366887,-15.162351,-6.357512 },
        { 8.394926,-2.960067, 22.292115, 9.524129 },
        { 7.803242,-2.080287, 19.217706, 8.186645 }
     };
 
   matrix eigen_vectors;
   vector eigen_values;
 
   bool res=matrix_a.Eig(eigen_vectors, eigen_values);
   Print("res=",res,"  error=",GetLastError());
   Print("Eigen vectors:\n",eigen_vectors, "\nEigen Values:\n",eigen_values);
 
//--- 检查正确性 A * v = lambda * v
   int vectors=0;
   for(ulong n=0; n<eigen_values.Size(); n++)
     {
      vector eigen_vector=eigen_vectors.Col(n);
      vector vector_d1   =eigen_vector*eigen_values[n];
      vector vector_d2   =matrix_a.MatMul(eigen_vector);
 
      ulong errors=vector_d1.Compare(vector_d2,1e-13);
      if(errors==0)
         vectors++;
     }
   Print("vectors=",vectors);
 
//--- 复解
   matrix<complex> eigen_vectors_c;
   vector<complex> eigen_values_c;
   ResetLastError();
   res=matrix_a.Eig(eigen_vectors_c,eigen_values_c);
   Print("res=",res,"  error=",GetLastError());
   Print("Eigen vectors:\n",eigen_vectors_c, "\nEigen Values:\n",eigen_values_c);
 
//--- 检查正确性 A * v = lambda * v
   matrixc matrix_c;
   matrix_c.Assign(matrix_a);
   vectors=0;
   for(ulong n=0; n<eigen_values_c.Size(); n++)
     {
      vectorc eigen_vector_c=eigen_vectors_c.Col(n);
      vectorc vector_c1     =eigen_vector_c*eigen_values_c[n];
      vectorc vector_c2     =matrix_c.MatMul(eigen_vector_c);
 
      ulong errors=vector_c1.Compare(vector_c2,1e-13);
      if(errors==0)
         vectors++;
     }
   Print("vectors=",vectors);
  }
/* Result
   res=true  error=4019
   Eigen vectors:
   [[0.2649667608713664]
    [0.4488818803991876]
    [-0.6527335897527492]
    [-0.5497604331807768]]
   Eigen Values:
   [28.94158645962942]
   vectors=1
   res=true  error=0
   Eigen vectors:
   [[(0.2649667608713664,0),(0.2227392219204762,0.3745470492013296),(0.403285439089771,-0.1345146135716524),(-0.2050778513598178,0)]
    [(0.4488818803991876,0),(-0.2613452530342438,-0.3685707727819327),(-0.3968506126372395,0.5257002255533059),(0.8014703373356256,0)]
    [(-0.6527335897527492,0),(-0.3418479634708521,-0.3299830378162041),(-0.3553021031180292,-0.03685418759727989),(-0.05618703726964112,0)]
    [(-0.5497604331807768,0),(0.523227993452828,0.3262508584080381),(0.3512835596143666,0.3666300350184092),(0.558955624442244,0)]]
   Eigen Values:
   [(28.94158645962942,0),(0.01022501104810897,0.02954980822331488),(0.01022501104810897,-0.02954980822331488),(0.4090215182743634,0)]
   vectors=3
*/

7.6.3 EigVals

计算一般矩阵的本征值。

bool matrix::EigVals(
  vector&  eigen_values      // 本征向量
   );

参数

eigen_values

[输出] 右本征值的向量。

返回值

成功时返回 true，否则返回 false。

注意

EigVals 和 Eig 之间的唯一区别是 EigVals 不计算本征向量，它只计算本征值。

7.6.4 LU

矩阵的 LU 因数分解为下三角矩阵和上三角矩阵的乘积。

bool matrix::LU(
  matrix&  L,     // 下三角矩阵
  matrix&  U      // 上三角矩阵
   );

参数

L 键

[输出] 下三角矩阵。

U

[输出] 上三角矩阵。

返回值

成功时返回 true，否则返回 false。

举例

   matrix matrix_a={{1,2,3,4},
                    {5,2,6,7},
                    {8,9,3,10},
                    {11,12,14,4}};
   matrix matrix_l,matrix_u;
//--- LU 分解
   matrix_a.LU(matrix_l,matrix_u);
   Print("matrix_l\n",matrix_l);
   Print("matrix_u\n",matrix_u);
//--- 验算是否 A = L * U
   Print("check\n",matrix_l.MatMul(matrix_u));
 
   /*
   matrix_l
   [[1,0,0,0]
    [5,1,0,0]
    [8,0.875,1,0]
    [11,1.25,0.5904761904761905,1]]
   matrix_u
   [[1,2,3,4]
    [0,-8,-9,-13]
    [0,0,-13.125,-10.625]
    [0,0,0,-17.47619047619047]]
   check
   [[1,2,3,4]
    [5,2,6,7]
    [8,9,3,10]
    [11,12,14,4]]
   */

7.6.5 LUP

具有部分轴的 LUP 因数分解，仅指具有行排列的 LU 分解：PA=LU。

bool  LUP(
  matrix&  L,     // 下三角矩阵
  matrix&  U,     // 上三角矩阵
  matrix&  P      // 排列矩阵
   );

参数

L 键

[输出] 下三角矩阵。

U

[输出] 上三角矩阵。

P

[out] Permutations matrix

返回值

成功时返回 true，否则返回 false。

举例

   matrix matrix_a={{1,2,3,4},
                    {5,2,6,7},
                    {8,9,3,10},
                    {11,12,14,4}};
   matrix matrix_l,matrix_u,matrix_p;
//--- LUP 分解
   matrix_a.LUP(matrix_l,matrix_u,matrix_p);
   Print("matrix_l\n",matrix_l);
   Print("matrix_u\n",matrix_u);
   Print("matrix_p\n",matrix_p);
//--- 验算是否 P * A = L * U
   Print("P * A\n",matrix_p.MatMul(matrix_a));
   Print("L * U\n",matrix_l.MatMul(matrix_u));
 
   /*
   matrix_l
   [[1,0,0,0]
    [0.4545454545454545,1,0,0]
    [0.7272727272727273,-0.07894736842105282,1,0]
    [0.09090909090909091,-0.2631578947368421,-0.2262773722627738,1]]
   matrix_u
   [[11,12,14,4]
    [0,-3.454545454545454,-0.3636363636363633,5.181818181818182]
    [0,0,-7.210526315789473,7.500000000000001]
    [0,0,0,6.697080291970803]]
   matrix_p
   [[0,0,0,1]
    [0,1,0,0]
    [0,0,1,0]
    [1,0,0,0]]
   P * A
   [[11,12,14,4]
    [5,2,6,7]
    [8,9,3,10]
    [1,2,3,4]]
   L * U
   [[11,12,14,4]
    [5,2,6,7]
    [8,9,3.000000000000001,10]
    [1,2,3,4]]
   */

7.6.6 QR

计算矩阵的 QR 分解。

bool  QR(
  matrix&  Q,     // 具有正交列的矩阵
  matrix&  R      // 上三角矩阵
   );

参数

Q

[输出] 具有正交列的矩阵。 当模式=“完成”时，结果是一个正交/酉矩阵，这取决于 a 是否是实数/复数。 在这种情况下，行列式可以是 +/- 1。 如果输入数组中的维数大于 2，则返回拥有上述属性的矩阵堆栈。

R 键

[输出] 上三角矩阵。

返回值

成功时返回 true，否则返回 false。

举例

//---  A*x = b
  matrix A = {{0, 1}, {1, 1}, {1, 1}, {2, 1}};
  Print("A \n", A);
  vector b = {1, 2, 2, 3};
  Print("b \n", b);
//--- A = Q*R
  matrix q, r;
  A.QR(q, r);
  Print("q \n", q);
  Print("r \n", r);
  matrix qr=q.MatMul(r);
  Print("qr \n", qr);
  /* 
  A
  [[0,1]
  [1,1]
  [1,1]
  [2,1]]
  b
  [1,2,2,3]
  q
  [[0.4082482904638631,-0.8164965809277259,-1.110223024625157e-16,-0.4082482904638631]
  [0.4625425214347352,-0.03745747856526496,0.7041241452319315,0.5374574785652647]
  [-0.5374574785652648,-0.03745747856526496,0.7041241452319316,-0.4625425214347352]
  [-0.5749149571305296,-0.5749149571305299,-0.09175170953613698,0.5749149571305296]]
  r
  [[-1.224744871391589,-0.2415816237971962]
  [-1.22474487139159,-1.466326495188786]
  [1.224744871391589,1.316496580927726]
  [1.224744871391589,0.2415816237971961]]
  qr
  [[-1.110223024625157e-16,1]
  [1,0.9999999999999999]
  [1,1]
  [2,1]]
  */

7.6.7 SVD

奇异值分解。

bool matrix::SVD(
  matrix&  U,                   // 酉矩阵
  matrix&  V,                   // 酉矩阵
  vector&  singular_values      // 奇异值向量
   );

参数

U

[输出] m 阶酉矩阵，由左奇异向量组成。

V

[输出] n 阶酉矩阵，由右奇异向量组成。

singular_values

[输出] 奇异值

返回值

成功时返回 true，否则返回 false。

举例

  matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
//--- 执行 SVD 分解
  matrix U, V;
  vector singular_values;
  b.SVD(U, V, singular_values);
  Print("U \n", U);
  Print("V \n", V);
  Print("singular_values = ", singular_values);
 
// 检查模块
//--- U * 奇异值对角线 * V = A
  matrix matrix_s;
  matrix_s.Diag(singular_values);
  Print("matrix_s \n", matrix_s);
  matrix matrix_vt=V.Transpose();
  Print("matrix_vt \n", matrix_vt);
  matrix matrix_usvt=(U.MatMul(matrix_s)).MatMul(matrix_vt);
  Print("matrix_usvt \n", matrix_usvt);
 
  ulong errors=(int)b.Compare(matrix_usvt, 1e-9);
  double res=(errors==0);
  Print("errors=", errors);
 
//---- 其它检查
  matrix U_Ut=U.MatMul(U.Transpose());
  Print("U_Ut \n", U_Ut);
  Print("Ut_U \n", (U.Transpose()).MatMul(U));
 
  matrix vt_V=matrix_vt.MatMul(V);
  Print("vt_V \n", vt_V);
  Print("V_vt \n", V.MatMul(matrix_vt));
 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
   [-1,0,1]
   [2,3,4]]
  U
  [[-0.7071067811865474,0.5773502691896254,0.408248290463863]
   [-6.827109697437648e-17,0.5773502691896253,-0.8164965809277256]
   [0.7071067811865472,0.5773502691896255,0.4082482904638627]]
  V
  [[0.5773502691896258,-0.7071067811865474,-0.408248290463863]
   [0.5773502691896258,1.779939029415334e-16,0.8164965809277258]
   [0.5773502691896256,0.7071067811865474,-0.408248290463863]]
  singular_values = [7.348469228349533,2.449489742783175,3.277709923350408e-17]
 
  matrix_s
  [[7.348469228349533,0,0]
   [0,2.449489742783175,0]
   [0,0,3.277709923350408e-17]]
  matrix_vt
  [[0.5773502691896258,0.5773502691896258,0.5773502691896256]
   [-0.7071067811865474,1.779939029415334e-16,0.7071067811865474]
   [-0.408248290463863,0.8164965809277258,-0.408248290463863]]
  matrix_usvt
  [[-3.999999999999997,-2.999999999999999,-2]
   [-0.9999999999999981,-5.977974170712231e-17,0.9999999999999974]
   [2,2.999999999999999,3.999999999999996]]
  errors=0
 
  U_Ut
  [[0.9999999999999993,-1.665334536937735e-16,-1.665334536937735e-16]
   [-1.665334536937735e-16,0.9999999999999987,-5.551115123125783e-17]
   [-1.665334536937735e-16,-5.551115123125783e-17,0.999999999999999]]
  Ut_U
  [[0.9999999999999993,-5.551115123125783e-17,-1.110223024625157e-16]
   [-5.551115123125783e-17,0.9999999999999987,2.498001805406602e-16]
   [-1.110223024625157e-16,2.498001805406602e-16,0.999999999999999]]
  vt_V
  [[1,-5.551115123125783e-17,0]
   [-5.551115123125783e-17,0.9999999999999996,1.110223024625157e-16]
   [0,1.110223024625157e-16,0.9999999999999996]]
  V_vt
  [[0.9999999999999999,1.110223024625157e-16,1.942890293094024e-16]
   [1.110223024625157e-16,0.9999999999999998,1.665334536937735e-16]
   [1.942890293094024e-16,1.665334536937735e-16,0.9999999999999996]
  */
 }

7.7 统计方法

计算矩阵和向量的描述性统计的方法。

函数	动作
ArgMax	返回最大值的索引
ArgMin	返回最小值的索引
Max	返回矩阵/向量中的最大值
Min	返回矩阵/向量中的最小值
Ptp	返回矩阵/向量或给定矩阵轴的数值范围
Sum	返回矩阵/矢量元素的总和，这些元素也可以针对给定轴（轴）执行
Prod	返回矩阵/矢量元素的乘积，也可以针对给定轴执行
CumSum	返回矩阵/矢量元素的累积总和，包括沿给定轴的矩阵/矢量元素
CumProd	返回矩阵/向量元素的累积乘积，包括沿给定轴的累积乘积
Percentile	返回矩阵/向量元素，或沿指定轴的元素值的指定百分位数
Quantile	返回矩阵/向量元素，或沿指定轴的元素值的指定分位数
Median	计算矩阵/向量元素的中位数
Mean	计算元素值的算术平均值
Average	计算矩阵/向量值的加权平均值
Std	返回矩阵/向量元素，或沿给定轴的元素值的标准偏差
Var	计算矩阵/向量元素值的方差
LinearRegression	计算包含计算的线性回归值的向量/矩阵

7.7.1 ArgMax

返回最大值的索引。

ulong vector::ArgMax();
 
ulong matrix::ArgMax();
 
vector matrix::ArgMax(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

最大值的索引。

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vector cols_max=matrix_a.ArgMax(0);
   vector rows_max=matrix_a.ArgMax(1);
   ulong  matrix_max=matrix_a.ArgMax();
 
   Print("cols_max=",cols_max);
   Print("rows_max=",rows_max);
   Print("max index ",matrix_max,"  max value ",matrix_a.Flat(matrix_max));
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_max=[0,3,1]
   rows_max=[0,2,0,1]
   max index 5  max value 12.0
   */

7.7.2 ArgMin

返回最小值的索引。

ulong vector::ArgMin();
 
ulong matrix::ArgMin();
 
vector matrix::ArgMin(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

最小值的索引。

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vector cols_min=matrix_a.ArgMin(0);
   vector rows_min=matrix_a.ArgMin(1);
   ulong  matrix_min=matrix_a.ArgMin();
 
   Print("cols_min=",cols_min);
   Print("rows_min=",rows_min);
   Print("min index ",matrix_min,"  min value ",matrix_a.Flat(matrix_min));
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_min=[1,0,0]
   rows_min=[2,0,2,0]
   min index 3  min value 1.0
   */

7.7.3 Max

返回矩阵/向量中的最大值。

double vector::Max();
 
double matrix::Max();
 
vector matrix::Max(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

矩阵/向量中的最大值。

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vector cols_max=matrix_a.Max(0);
   vector rows_max=matrix_a.Max(1);
   double matrix_max=matrix_a.Max();
 
   Print("cols_max=",cols_max);
   Print("rows_max=",rows_max);
   Print("max value ",matrix_max);
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_max=[10,11,12]
   rows_max=[10,12,6,11]
   max value 12.0
   */

7.7.4 Min

返回矩阵/向量中的最小值。

double vector::Min();
 
double matrix::Min();
 
vector matrix::Min(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

矩阵/向量中的最小值。

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vector cols_min=matrix_a.Min(0);
   vector rows_min=matrix_a.Min(1);
   double matrix_min=matrix_a.Min();
 
   Print("cols_min=",cols_min);
   Print("rows_min=",rows_min);
   Print("min value ",matrix_min);
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_min=[1,3,2]
   rows_min=[2,1,4,7]
   min value 1.0
   */

7.7.5 Ptp

返回矩阵/向量或给定矩阵轴的数值范围，等效于 Max() - Min()。 Ptp - 峰值到峰值。

double vector::Ptp();
 
double matrix::Ptp();
 
vector matrix::Ptp(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

向量的数值范围（最大值 - 最小值）

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vector cols_ptp=matrix_a.Ptp(0);
   vector rows_ptp=matrix_a.Ptp(1);
   double matrix_ptp=matrix_a.Ptp();
 
   Print("cols_ptp  ",cols_ptp);
   Print("rows_ptp  ",rows_ptp);
   Print("ptp value  ",matrix_ptp);
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_ptp [9,8,10]
   rows_ptp [8,11,2,4]
   ptp value  11.0
   */

7.7.6 Sum

返回矩阵/矢量元素的总和，这些元素也可以针对给定轴（轴）执行。

double vector::Sum();
 
double matrix::Sum();
 
vector matrix::Sum(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

矩阵/矢量元素的总和，也可以针对给定轴（轴）执行。

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vector cols_sum=matrix_a.Sum(0);
   vector rows_sum=matrix_a.Sum(1);
   double matrix_sum=matrix_a.Sum();
 
   Print("cols_sum=",cols_sum);
   Print("rows_sum=",rows_sum);
   Print("sum value ",matrix_sum);
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_sum=[24,27,27]
   rows_sum=[15,21,15,27]
   sum value 78.0
   */

7.7.7 Prod

返回矩阵/矢量元素的乘积，该乘积也可以针对给定轴执行。

double vector::Prod(
  const double  initial=1      // initial multiplier
   );
 
double matrix::Prod(
  const double  initial=1      // initial multiplier
   );
 
vector matrix::Prod(
  const int     axis,          // axis
  const double  initial=1      // initial multiplier
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

initial=1

[输入] 初始乘数。

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vector cols_prod=matrix_a.Prod(0);
   vector rows_prod=matrix_a.Prod(1);
   double matrix_prod=matrix_a.Prod();
 
   Print("cols_prod=",cols_prod);
   cols_prod=matrix_a.Prod(0,0.1);
   Print("cols_prod=",cols_prod);
   Print("rows_prod=",rows_prod);
   Print("prod value ",matrix_prod);
 
  /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_prod=[420,1320,864]
   cols_prod=[42,132,86.40000000000001]
   rows_prod=[60,96,120,693]
   prod value 479001600.0
  */

7.7.8 CumSum

返回矩阵/矢量元素的累积总和，包括沿给定轴的元素。

vector vector::CumSum();
 
vector matrix::CumSum();
 
matrix matrix::CumSum(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

沿给定轴的元素的累积总和。

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   matrix cols_cumsum=matrix_a.CumSum(0);
   matrix rows_cumsum=matrix_a.CumSum(1);
   vector cumsum_values=matrix_a.CumSum();
 
   Print("cols_cumsum\n",cols_cumsum);
   Print("rows_cumsum\n",rows_cumsum);
   Print("cumsum values  ",cumsum_values);
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_cumsum
   [[10,3,2]
    [11,11,14]
    [17,16,18]
    [24,27,27]]
   rows_cumsum
   [[10,13,15]
    [1,9,21]
    [6,11,15]
    [7,18,27]]
   cumsum values  [10,13,15,16,24,36,42,47,51,58,69,78]
   */

7.7.9 CumProd

返回矩阵/向量元素的累积乘积，包括沿给定轴的累积乘积。

vector vector::CumProd();
 
vector matrix::CumProd();
 
matrix matrix::CumProd(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 每列的水平轴（即，整行），1 ― 每行的垂直轴（即，整列）

返回值

元素沿给定轴的累积乘积。

举例

   matrix matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   matrix cols_cumprod=matrix_a.CumProd(0);
   matrix rows_cumprod=matrix_a.CumProd(1);
   vector cumprod_values=matrix_a.CumProd();
 
   Print("cols_cumprod\n",cols_cumprod);
   Print("rows_cumprod\n",rows_cumprod);
   Print("cumprod values  ",cumprod_values);
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_cumprod
   [[10,3,2]
    [10,24,24]
    [60,120,96]
    [420,1320,864]]
   rows_cumprod
   [[10,30,60]
    [1,8,96]
    [6,30,120]
    [7,77,693]]
   cumprod values  [10,30,60,60,480,5760,34560,172800,691200,4838400,53222400,479001600]
   */

7.7.10 Percentile

返回矩阵/矢量元素或沿指定轴的元素值的指定百分位数。

double vector::Percentile(
  const int  percent      // 
   );
 
double matrix::Percentile(
  const int  percent      // 
   );
 
vector matrix::Percentile(
  const int  percent,     // 
  const int  axis         // axis
   );

参数

percent

[输入] 欲计算的百分位数，必须介于 0 和 100（含）之间。

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

百分位数：标量或向量。

注意

“percent” 参数的有效值范围在 [0, 100] 之内。 采用线性算法计算百分位数。 正确计算中位数需要对序列进行排序。

举例

   matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_percentile=matrix_a.Percentile(50,0);
   vectorf rows_percentile=matrix_a.Percentile(50,1);
   float matrix_percentile=matrix_a.Percentile(50);
 
   Print("cols_percentile ",cols_percentile);
   Print("rows_percentile ",rows_percentile);
   Print("percentile value  ",matrix_percentile);
 
 
   /*
   matrix_a
   [[1,2,3]
    [4,5,6]
    [7,8,9]
    [10,11,12]]
   cols_percentile [5.5,6.5,7.5]
   rows_percentile [2,5,8,11]
   percentile value  6.5
   */

7.7.11 Quantile

返回矩阵/矢量元素或沿指定轴元素值的分位数。

double vector::Quantile(
  const double quantile      // quantile
   );
 
double matrix::Quantile(
  const double quantile      // quantile
   );
 
vector matrix::Quantile(
  const double quantile,     // quantile
  const int    axis          // axis
   );

参数

quantile

[输入] 欲计算的分位数，必须介于 0 和 1（含）之间。

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

分位数：标量或向量。

注意

'quantile' 参数取值范围 [0, 1]。 采用线性算法计算分位数。 正确计算分位数需要对序列进行排序。

举例

   matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_quantile=matrix_a.Quantile(0.5,0);
   vectorf rows_quantile=matrix_a.Quantile(0.5,1);
   float matrix_quantile=matrix_a.Quantile(0.5);
 
   Print("cols_quantile ",cols_quantile);
   Print("rows_quantile ",rows_quantile);
   Print("quantile value  ",matrix_quantile);
 
   /*
   matrix_a
   [[1,2,3]
    [4,5,6]
    [7,8,9]
    [10,11,12]]
   cols_quantile [5.5,6.5,7.5]
   rows_quantile [2,5,8,11]
   quantile value  6.5
   */

7.7.12 Median

计算矩阵/矢量元素的中位数。

double vector::Median();
 
double matrix::Median();
 
vector matrix::Median(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

中位数：标量或矢量。

注意

中位数是将数组/向量元素的最高一半与元素的最低一半分开的中间值。 与分位数（0.5）和百分位数（50）相同。 正确计算中位数需要对序列进行排序。

举例

   matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_median=matrix_a.Median(0);
   vectorf rows_median=matrix_a.Median(1);
   float matrix_median=matrix_a.Median();
 
   Print("cols_median ",cols_median);
   Print("rows_median ",rows_median);
   Print("median value  ",matrix_median);
 
 
   /*
   matrix_a
   [[1,2,3]
    [4,5,6]
    [7,8,9]
    [10,11,12]]
   cols_median [5.5,6.5,7.5]
   rows_median [2,5,8,11]
   median value  6.5
   */

7.7.13 Mean

计算元素值的算术平均值。

double vector::Mean();
 
double matrix::Mean();
 
vector matrix::Mean(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

元素值的算术平均值。

举例

   matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_mean=matrix_a.Mean(0);
   vectorf rows_mean=matrix_a.Mean(1);
   float matrix_mean=matrix_a.Mean();
 
   Print("cols_mean ",cols_mean);
   Print("rows_mean ",rows_mean);
   Print("mean value  ",matrix_mean);
 
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_mean [6,6.75,6.75]
   rows_mean [5,7,5,9]
   mean value  6.5
   */

7.7.14 Average

计算矩阵/向量值的加权平均值。

double vector::Average(
  const vector& weigts      // weights vector
   );
 
double matrix::Average(
  const matrix& weigts      // weights matrix
);
 
vector matrix::Average(
  const matrix& weigts,     // weights matrix
  const int     axis        // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

算术平均值：标量或向量。

注意

权重矩阵/向量与主矩阵/向量相关联。

举例

   matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   matrixf matrix_w=matrixf::Ones(4,3);
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_average=matrix_a.Average(matrix_w,0);
   vectorf rows_average=matrix_a.Average(matrix_w,1);
   float matrix_average=matrix_a.Average(matrix_w);
 
   Print("cols_average ",cols_average);
   Print("rows_average ",rows_average);
   Print("average value  ",matrix_average);
 
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_average [6,6.75,6.75]
   rows_average [5,7,5,9]
   average value  6.5
   */ value  6.5

7.7.15 Std

返回矩阵/矢量元素或沿给定轴的元素值的标准偏差。

double vector::Std();
 
double matrix::Std();
 
vector matrix::Std(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

Standard_deviation: 标量或矢量。

注意

标准差是与平均值的平方偏差平均值的平方根， 即，std = sqrt(mean(x))，其中 x = abs(a - a.mean())**2。

典型的平均平方偏差计算为 x.sum() / N，其中 N = len(x)。

举例

   matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_std=matrix_a.Std(0);
   vectorf rows_std=matrix_a.Std(1);
   float matrix_std=matrix_a.Std();
 
   Print("cols_std ",cols_std);
   Print("rows_std ",rows_std);
   Print("std value  ",matrix_std);
 
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_std [3.2403703,3.0310888,3.9607449]
   rows_std [3.5590262,4.5460606,0.81649661,1.6329932]
   std value  3.452052593231201
   */

7.7.16 Var

计算矩阵/向量元素值的方差。

double vector::Var();
 
double matrix::Var();
 
vector matrix::Var(
  const int  axis      // axis
   );

参数

axis

[输入] 轴。 0 ― 水平轴，1 ― 垂直轴。

返回值

方差：标量或向量。

注意

方差是与平均值的平方偏差的平均值，即，var = mean(x), where x = abs(a - a.mean())**2。

平均值的典型计算为 x.sum() / N，其中 N = len(x)。

举例

   matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_var=matrix_a.Var(0);
   vectorf rows_var=matrix_a.Var(1);
   float matrix_var=matrix_a.Var();
 
   Print("cols_var ",cols_var);
   Print("rows_var ",rows_var);
   Print("var value  ",matrix_var);
 
 
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_var [10.5,9.1875,15.6875]
   rows_var [12.666667,20.666666,0.66666669,2.6666667]
   var value  11.916666984558105
   */

7.7.17 LinearRegression

计算包含计算的线性回归值的向量/矩阵。

vector vector::LinearRegression();
 
matrix matrix::LinearRegression(
  ENUM_MATRIX_AXIS  axis=AXIS_NONE      // 沿其计算回归的轴线
   );

参数

axis

[in] 指定沿其计算回归的轴线。ENUM_MATRIX_AXIS枚举值(AXIS_HORZ ― 横轴， AXIS_VERT ― 竖轴)。

返回值

包含计算的线性回归值的向量/矩阵。

注意

使用标准回归方程计算线性回归：y (x) = a * x + b，其中a是直线斜率，而b是其Y轴位移。

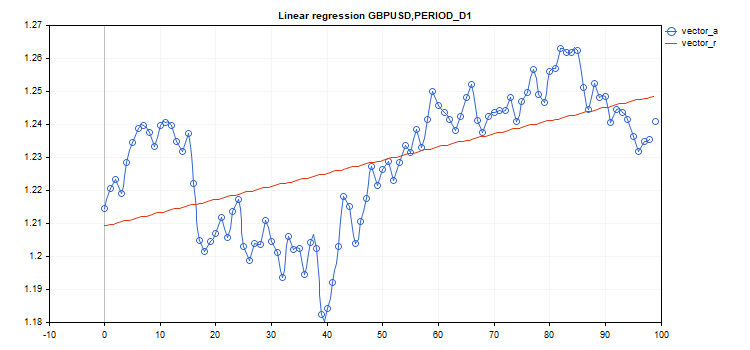
示例：

#include <Graphics\Graphic.mqh>
 
#define GRAPH_WIDTH  750
#define GRAPH_HEIGHT 350
 
//+------------------------------------------------------------------+
//| 脚本程序起始函数                                                   |
//+------------------------------------------------------------------+
void OnStart()
  {
   vector vector_a;
   vector_a.CopyRates(_Symbol,_Period,COPY_RATES_CLOSE,1,100);
   vector vector_r=vector_a.LinearRegression();
 
//--- 关闭图表显示
   ChartSetInteger(0,CHART_SHOW,false);
 
//--- 用于绘制图形的数组
   double x[];
   double y1[];
   double y2[];
   ArrayResize(x,uint(vector_a.Size()));
   ArrayResize(y1,uint(vector_a.Size()));
   ArrayResize(y2,uint(vector_a.Size()));
   for(ulong i=0; i<vector_a.Size(); i++)
     {
      x[i]=(double)i;
      y1[i]=vector_a[i];
      y2[i]=vector_r[i];
     }
 
//--- 图形标题
   string title="Linear regression "+_Symbol+","+EnumToString(_Period);
 
   long   chart=0;
   string name="LinearRegression";
 
//--- 创建图形
   CGraphic graphic;
   graphic.Create(chart,name,0,0,0,GRAPH_WIDTH,GRAPH_HEIGHT);
   graphic.BackgroundMain(title);
   graphic.BackgroundMainSize(12);
   
//--- 激活函数图
   CCurve *curvef=graphic.CurveAdd(x,y1,CURVE_POINTS_AND_LINES);
   curvef.Name("vector_a");
   curvef.LinesWidth(2);
   curvef.LinesSmooth(true);
   curvef.LinesSmoothTension(1);
   curvef.LinesSmoothStep(10);
 
//--- 激活函数的导数
   CCurve *curved=graphic.CurveAdd(x,y2,CURVE_LINES);
   curved.Name("vector_r");
   curved.LinesWidth(2);
   curved.LinesSmooth(true);
   curved.LinesSmoothTension(1);
   curved.LinesSmoothStep(10);
   graphic.CurvePlotAll();
   graphic.Update();
 
//--- 无限循环识别按下的键盘按键
   while(!IsStopped())
     {
      //--- 按下escape键退出程序
      if(TerminalInfoInteger(TERMINAL_KEYSTATE_ESCAPE)!=0)
         break;
      //--- 按下PdDn保存图形图片
      if(TerminalInfoInteger(TERMINAL_KEYSTATE_PAGEDOWN)!=0)
        {
         string file_names[];
         if(FileSelectDialog("Save Picture",NULL,"All files (*.*)|*.*",FSD_WRITE_FILE,file_names,"LinearRegression.png")<1)
            continue;
         ChartScreenShot(0,file_names[0],GRAPH_WIDTH,GRAPH_HEIGHT);
        }
      Sleep(10);
     }
 
//--- 清除
   graphic.Destroy();
   ObjectDelete(chart,name);
   ChartSetInteger(0,CHART_SHOW,true);
  }

ENUM_MATRIX_AXIS

用于在矩阵所有统计函数中指定轴线的枚举。

ID	描述
AXIS_NONE	没有指定坐标轴。对所有矩阵元素执行计算，类似向量(请参见Flat方法)。
AXIS_HORZ	横轴
AXIS_VERT	竖轴

7.8 特征方法

这些方法可以接收矩阵特征，诸如：

• 行数
• 列数
• 范数
• 条件数字
• 行列式
• 矩阵的秩
• 迹线
• 谱

函数	动作
Rows	返回矩阵中的行数
Cols	返回矩阵中的列数
Size	返回向量的大小
Norm	返回矩阵或向量范数
Cond	计算一个矩阵的条件数
Det	计算平方可逆矩阵的行列式
SLogDet	计算矩阵行列式的符号和对数
Rank	返回利用高斯（Gaussian）方法的矩阵秩
Trace	返回矩阵对角线的总和
Spectrum	计算矩阵的谱作为其本征值的集合，来自乘积 AT*A

7.8.1 Rows

返回矩阵中的行数。

ulong matrix::Rows()

返回值

整数。

举例

  matrix m= {{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}};
  m.Reshape(3, 4);
  Print("matrix m \n" , m);
  Print("m.Rows()=", m.Rows());
  Print("m.Cols()=", m.Cols());
 
  /*
   matrix m 
   [[1,2,3,4]
    [5,6,7,8]
    [9,10,11,12]]
   m.Rows()=3
   m.Cols()=4
  */

7.8.2 Cols

返回矩阵中的列数。

ulong matrix::Cols()

返回值

整数。

举例

  matrix m= {{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}};
  m.Reshape(3, 4);
  Print("matrix m \n" , m);
  Print("m.Cols()=", m.Cols());
  Print("m.Rows()=", m.Rows());
 
  /*
   matrix m 
   [[1,2,3,4]
    [5,6,7,8]
    [9,10,11,12]]
   m.Cols()=4
   m.Rows()=3
  */

7.8.3 Size

返回向量的大小。

ulong vector::Size()

返回值

整数。

举例

  matrix m={{1,2,3,4,5,6,7,8,9,10,11,12}};
  m.Reshape(3,4);
  Print("matrix m\n",m);
  vector v=m.Row(1);
  Print("v.Size()=",v.Size());
  Print("v=",v);
 
 
  /*
   matrix m
   [[1,2,3,4]
    [5,6,7,8]
    [9,10,11,12]]
   v.Size()=4
   v=[5,6,7,8]  
  */

7.8.4 Norm

返回矩阵或向量的范数。

double vector::Norm(
  const ENUM_VECTOR_NORM  norm,     // 向量范数
  const int                        norm_p=2  // p-范数，如果是 VECTOR_NORM_P
   );
 
double matrix::Norm(
  const ENUM_MATRIX_NORM  norm      // 矩阵范数
   );

参数

范数

[输入] 范数顺序

返回值

矩阵或向量的范数。

注意

• VECTOR_NORM_INF 是向量元素中的最大绝对值。
• VECTOR_NORM_MINUS_INF 是向量元素中的最小绝对值。
• VECTOR_NORM_P 是向量的 P-范数。 如果 norm_p=0，那么这是非零向量元素的数量。 norm_p=1 是矢量元素绝对值的总和。 norm_p=2 是向量元素值平方和的平方根。 P-范数可以为负值。
• MATRIX_NORM_FROBENIUS 是矩阵元素值的平方和的平方根。 弗罗贝尼乌斯（Frobenius）范数和向量 P2-范数是一致的。
• MATRIX_NORM_SPECTRAL 是矩阵谱的最大值。
• MATRIX_NORM_NUCLEAR 是矩阵奇异值的总和。
• MATRIX_NORM_INF 是矩阵垂直向量中的最大向量 p1-范数。 矩阵 inf-范数和向量 inf-范数是一致的。
• MATRIX_NORM_MINUS_INF 是矩阵垂直向量中的最小向量 p1-范数。
• MATRIX_NORM_P1 是矩阵水平向量中的最大向量 p1-范数。
• MATRIX_NORM_MINUS_P1 是矩阵水平向量中的最小向量 p1-范数。
• MATRIX_NORM_P2 是矩阵的最高奇异值。
• MATRIX_NORM_MINUS_P2 是矩阵的最低奇异值。

以 MQL5 实现的计算向量 P-范数的简单算法：

double VectorNormP(const vector& v,int norm_value)
  {
   ulong  i;
   double norm=0.0;
//---
   switch(norm_value)
     {
      case 0 :
         for(i=0; i<v.Size(); i++)
            if(v[i]!=0)
               norm+=1.0;
         break;
      case 1 :
         for(i=0; i<v.Size(); i++)
            norm+=MathAbs(v[i]);
         break;
      case 2 :
         for(i=0; i<v.Size(); i++)
            norm+=v[i]*v[i];
         norm=MathSqrt(norm);
         break;
      default :
         for(i=0; i<v.Size(); i++)
            norm+=MathPow(MathAbs(v[i]),norm_value);
         norm=MathPow(norm,1.0/norm_value);
     }
//---
   return(norm);
  }

MQL5 示例:

  matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_FROBENIUS)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_INF)", b.Norm(MATRIX_NORM_INF));
  Print("b.Norm(MATRIX_NORM_MINUS_INF)", b.Norm(MATRIX_NORM_MINUS_INF));
  Print("b.Norm(MATRIX_NORM_P1)=)", b.Norm(MATRIX_NORM_P1));
  Print("b.Norm(MATRIX_NORM_MINUS_P1)=", b.Norm(MATRIX_NORM_MINUS_P1));
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_P2));
  Print("b.Norm(MATRIX_NORM_MINUS_P2)=", b.Norm(MATRIX_NORM_MINUS_P2));
 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
  [-1,0,1]
  [2,3,4]]
  b.Norm(MATRIX_NORM_P2)=7.745966692414834
  b.Norm(MATRIX_NORM_FROBENIUS)=7.745966692414834
  b.Norm(MATRIX_NORM_INF)9.0
  b.Norm(MATRIX_NORM_MINUS_INF)2.0
  b.Norm(MATRIX_NORM_P1)=)7.0
  b.Norm(MATRIX_NORM_MINUS_P1)=6.0
  b.Norm(MATRIX_NORM_P2)=7.348469228349533
  b.Norm(MATRIX_NORM_MINUS_P2)=1.857033188519056e-16
  */

Python 示例:

import numpy as np
from numpy import linalg as LA
a = np.arange(9) - 4
print("a \n",a)
b = a.reshape((3, 3))
print("b \n",b)
print("LA.norm(b)=",LA.norm(b))
print("LA.norm(b, 'fro')=",LA.norm(b, 'fro'))
print("LA.norm(b, np.inf)=",LA.norm(b, np.inf))
print("LA.norm(b, -np.inf)=",LA.norm(b, -np.inf))
print("LA.norm(b, 1)=",LA.norm(b, 1))
print("LA.norm(b, -1)=",LA.norm(b, -1))
print("LA.norm(b, 2)=",LA.norm(b, 2))
print("LA.norm(b, -2)=",LA.norm(b, -2))
 
a 
 [-4 -3 -2 -1  0  1  2  3  4]
b 
 [[-4 -3 -2]
 [-1  0  1]
 [ 2  3  4]]
LA.norm(b)= 7.745966692414834
LA.norm(b, 'fro')= 7.745966692414834
LA.norm(b, np.inf)= 9.0
LA.norm(b, -np.inf)= 2.0
LA.norm(b, 1)= 7.0
LA.norm(b, -1)= 6.0
LA.norm(b, 2)= 7.3484692283495345
LA.norm(b, -2)= 1.857033188519056e-16

7.8.5 Cond

计算矩阵的条件数。

double matrix::Cond(
  const ENUM_MATRIX_NORM  norm      // 矩阵范数
   );

参数

范数

[输入] 来自 ENUM_MATRIX_NORM 的范数顺序

返回值

矩阵的条件数字。 也许是无限的。

注意

x 的条件数定义为 x 的范数乘以 x 的逆范数 [1]。 范数可以是通常的 L2-范数（平方和的根），或许多其它矩阵范数之一。

条件数 K 值，等于矩阵 A 的范数及其逆的乘积。 条件数太高的矩阵称为病态。 条件数较低的称为良态。 逆矩阵采用伪反演得到，不受矩阵的直点和非奇点条件的限制。

谱条件数是一个例外。

以 MQL5 实现的计算谱条件数的简单算法：

double MatrixCondSpectral(matrix& a)
  {
   double norm=0.0;
   vector v=a.Spectrum();
 
   if(v.Size()>0)
     {
      double max_norm=v[0];
      double min_norm=v[0];
      for(ulong i=1; i<v.Size(); i++)
        {
         double real=MathAbs(v[i]);
         if(max_norm<real)
            max_norm=real;
         if(min_norm>real)
            min_norm=real;
        }
      max_norm=MathSqrt(max_norm);
      min_norm=MathSqrt(min_norm);
      if(min_norm>0.0)
         norm=max_norm/min_norm;
     }
 
   return(norm);
  }

MQL5 示例:

  matrix a= {{1, 0, -1}, {0, 1, 0}, { 1, 0, 1}};
  Print("a.Cond(MATRIX_NORM_P2)=", a.Cond(MATRIX_NORM_P2));
  Print("a.Cond(MATRIX_NORM_FROBENIUS)=", a.Cond(MATRIX_NORM_FROBENIUS));
  Print("a.Cond(MATRIX_NORM_INF)=", a.Cond(MATRIX_NORM_INF));
  Print("a.Cond(MATRIX_NORM_MINUS_INF)=", a.Cond(MATRIX_NORM_MINUS_INF));
  Print("a.Cond(MATRIX_NORM_P1)=)", a.Cond(MATRIX_NORM_P1));
  Print("a.Cond(MATRIX_NORM_MINUS_P1)=", a.Cond(MATRIX_NORM_MINUS_P1));
  Print("a.Cond(MATRIX_NORM_P2)=", a.Cond(MATRIX_NORM_P2));
  Print("a.Cond(MATRIX_NORM_MINUS_P2)=", a.Cond(MATRIX_NORM_MINUS_P2));
 
  /*
  matrix a
  [[1,0,-1]
  [0,1,0]
  [1,0,1]]
  a.Cond(MATRIX_NORM_P2)=1.414213562373095
  a.Cond(MATRIX_NORM_FROBENIUS)=3.162277660168379
  a.Cond(MATRIX_NORM_INF)=2.0
  a.Cond(MATRIX_NORM_MINUS_INF)=0.9999999999999997
  a.Cond(MATRIX_NORM_P1)=)2.0
  a.Cond(MATRIX_NORM_MINUS_P1)=0.9999999999999998
  a.Cond(MATRIX_NORM_P2)=1.414213562373095
  a.Cond(MATRIX_NORM_MINUS_P2)=0.7071067811865472
  */

Python 示例:

import numpy as np
from numpy import linalg as LA
a = np.array([[1, 0, -1], [0, 1, 0], [1, 0, 1]])
print("a \n",a)
print("LA.cond(a)=",LA.cond(a))
print("LA.cond(a, 'fro')=",LA.cond(a, 'fro'))
print("LA.cond(a, np.inf)=",LA.cond(a, np.inf))
print("LA.cond(a, -np.inf)=",LA.cond(a, -np.inf))
print("LA.cond(a, 1)=",LA.cond(a, 1))
print("LA.cond(a, -1)=",LA.cond(a, -1))
print("LA.cond(a, 2)=",LA.cond(a, 2))
print("LA.cond(a, -2)=",LA.cond(a, -2))
 
a 
 [[ 1  0 -1]
 [ 0  1  0]
 [ 1  0  1]]
LA.cond(a)= 1.4142135623730951
LA.cond(a, 'fro')= 3.1622776601683795
LA.cond(a, np.inf)= 2.0
LA.cond(a, -np.inf)= 1.0
LA.cond(a, 1)= 2.0
LA.cond(a, -1)= 1.0
LA.cond(a, 2)= 1.4142135623730951
LA.cond(a, -2)= 0.7071067811865475

7.8.6 Det

计算正方形可逆矩阵的行列式。

double matrix::Det()

返回值

矩阵的行列式。

注意

二阶和三阶矩阵行列式根据萨鲁斯（Sarrus）规则进行计算。 d2=a11a22-a12a21; d3=a11a22a33+a12a23a31+a13a21a32-a13a22a31-a11a23a32-a12a21a33

行列式是利用高斯（Gaussian）方法将矩阵简化为上三角形计算出的。 上三角矩阵的行列式等于主对角线元素的乘积。

如果至少一个矩阵的行或列为零，则行列式为零。

如果两个或多个矩阵的行或列线性相关，则其行列式为零。

矩阵的行列式等于其本征值的乘积。

MQL5 示例:

   matrix m={{1,2},{3,4}};
   double det=m.Det();
   Print("matrix m\n",m);
   Print("det(m)=",det);
   /*
   matrix m
   [[1,2]
    [3,4]]
   det(m)=-2.0      
   */

Python 示例:

import numpy as np
 
a = np.array([[1, 2], [3, 4]])
print('a \n',a)
print('nnp.linalg.det(a) \n',np.linalg.det(a))
 
a 
 [[1 2]
 [3 4]]
 
np.linalg.det(a) 
 -2.0000000000000004

7.8.7 SLogDet

计算矩阵行列式的符号和对数。

double matrix::SLogDet(
  int&  sign      // 符号
   );

参数

sign

[输出] 行列式的符号。 如果符号为偶数，则行列式为正数。

返回值

表示行列式符号的数字。

注意

行列式是利用高斯（Gaussian）方法将矩阵简化为上三角形计算出的。 上三角矩阵的行列式等于主对角线元素的乘积。 乘积的对数等于对数之和。 因此，如果在计算行列式时出现溢出，则可以使用 SLogDet 方法。

如果符号为偶数，则行列式为正数。

举例

a = np.array([[1, 2], [3, 4]])  
(sign, logdet) = np.linalg.slogdet(a)  
(sign, logdet) (-1, 0.69314718055994529) # may vary  sign * np.exp(logdet) -2.0

7.8.8 Rank

利用高斯（Gaussian）方法返回矩阵的秩。

int  Rank()

返回值

矩阵的秩。

注意

具有 m 行和 n 列的矩阵 A 的行（或列）系统的秩是线性独立行（或列）的最大数目。 如果若干行（列）中无一可用其它行（列）线性表达，则称为线性独立。 行系统的秩始终等于列系统的秩。 此值称为矩阵的秩。

MQL5 示例:

  matrix a=matrix::Eye(4, 4);;
  Print("matrix a \n", a);
  Print("a.Rank()=", a.Rank());
 
  matrix I=matrix::Eye(4, 4);
  I[3, 3] = 0.;    // 无秩矩阵
  Print("I \n", I);
  Print("I.Rank()=", I.Rank());
 
  matrix b=matrix::Ones(1, 4);
  Print("b \n", b);
  Print("b.Rank()=", b.Rank());;// 1 维 - 秩为 1 除外所有 0
 
  matrix  zeros=matrix::Zeros(4, 1);
  Print("zeros \n", zeros);
  Print("zeros.Rank()=", zeros.Rank());
 
  /*
  matrix a
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,1]]
  a.Rank()=4
 
  I
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,0]]
  I.Rank()=3
 
  b
  [[1,1,1,1]]
  b.Rank()=1
 
  zeros
  [[0]
  [0]
  [0]
  [0]]
  zeros.Rank()=0
  */

Python 示例:

import numpy as np
from numpy.linalg import matrix_rank
a=(np.eye(4)) # 全 秩 矩阵
print("a \n", a)
print("matrix_rank(a)=",matrix_rank(a))
I=np.eye(4)
I[-1,-1] = 0. # 秩 缺乏 矩阵x
print("I \n",I)
print("matrix_rank(I)=",matrix_rank(I))
 
b=np.ones((4,))
print("b \n",b)
print("matrix_rank(b)=",matrix_rank(b)) # 1 维 - 秩为 1 除外 全部 0
 
zeros=np.zeros((4,))
print("zeroes \n",zeros)
print("matrix_rank(zeros)=",matrix_rank(zeros))
 
a 
 [[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 1.]]
matrix_rank(a)= 4
 
I 
 [[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 0.]]
matrix_rank(I)= 3
 
b 
 [1. 1. 1. 1.]
matrix_rank(b)= 1
 
zeroes 
 [0. 0. 0. 0.]
matrix_rank(zeros)= 0

7.8.9 Trace

返回沿矩阵对角线的总和。 double matrix::Trace()

返回值

沿对角线的总和。

注意

矩阵的迹线等于其本征值的总和。

MQL5 示例:

  matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a.Reshape(3, 3);
  Print("matrix a \n", a);
  Print("a.Trace() \n", a.Trace());
 
  /*
  matrix a
  [[0,1,2]
  [3,4,5]
  [6,7,8]]
  a.Trace()
  12.0
  */

Python 示例:

a = np.arange(9).reshape((3,3))
print('a \n',a)
print('np.trace(a) \n',np.trace(a))
 
a 
 [[0 1 2]
 [3 4 5]
 [6 7 8]]
 
np.trace(a) 
 12

7.8.10 Spectrum

计算矩阵的谱，作为来自乘积 AT*A 的本征值集合。

vector matrix::Spectrum()

返回值

矩阵的谱作为矩阵本征值的向量。

举例

double MatrixCondSpectral(matrix& a)
  {
   double norm=0.0;
   vector v=a.Spectrum();
 
   if(v.Size()>0)
     {
      double max_norm=v[0];
      double min_norm=v[0];
      for(ulong i=1; i<v.Size(); i++)
        {
         double real=MathAbs(v[i]);
         if(max_norm<real)
            max_norm=real;
         if(min_norm>real)
            min_norm=real;
        }
      max_norm=MathSqrt(max_norm);
      min_norm=MathSqrt(min_norm);
      if(min_norm>0.0)
         norm=max_norm/min_norm;
     }
 
   return(norm);
  }

7.9 求解线性方程组的矩阵方法

求解线性方程组和计算逆矩阵的方法。

函数	动作
Solve	求解线性矩阵方程或线性代数方程组
LstSq	返回线性代数方程的最小二乘解（对于非二乘或退化矩阵）
Inv	通过乔丹-高斯（Jordan-Gauss）方法计算平方非退化矩阵的（乘法）逆
PInv	遵照摩尔-彭罗斯（Moore-Penrose）方法计算矩阵的伪逆

7.9.1 Solve

求解线性矩阵方程或线性代数方程组。

vector matrix::Solve(
  const vector  b      // 纵坐标或“因变量”值
   );

参数

b

[输入] 纵坐标或“因变量”值。 （自由项的向量）。

返回值

含有系统 a * x = b 之解的向量。

注意

如果至少一个矩阵行或列为零，则系统无解。

如果两个或多个矩阵行或列线性依赖，则系统无解。

举例

//--- SLAE 解法
   vector_x=matrix_a.Solve(vector_b);
//--- 检查是否 a * x = b
   result_vector=matrix_a.MatMul(vector_x);
   errors=vector_b.Compare(result_vector,1e-12);

7.9.2 LstSq

返回线性代数方程的最小二乘解（对于非二乘或退化矩阵）。

vector matrix::LstSq(
  const vector  b      // 纵坐标或“因变量”值
   );

参数

b

[输入] 纵坐标或“因变量”值。 （自由项的向量）

返回值

含有系统 a * x = b 之解的向量。 这仅适用于具有精准解的系统。

举例

   matrix a={{3, 2},
             {4,-5},
             {3, 3}};
   vector b={7,40,3};
//---
   vector x=a.LstSq(b);
//--- 检查，必须是 [5, -4]
   Print("x=", x);
//--- 检查，必须是 [7, 40, 3]
   vector b1=a.MatMul(x);
   Print("b1=",b1);
 
/*
  x=[5.000000000000002,-4]
  b1=[7.000000000000005,40.00000000000001,3.000000000000005]
*/

7.9.3 Inv

通过乔丹-高斯（Jordan-Gauss）方法计算平方可逆矩阵的乘法逆。

matrix matrix::Inv()

返回值

矩阵的乘法逆。

注意

原始矩阵和逆矩阵的乘积就是单位矩阵。

如果至少一个矩阵行或列为零，则无法获得逆矩阵。

如果两个或多个矩阵行或列线性依赖，则无法获得逆矩阵。

举例

int TestInverse(const int size_m)
  {
   int    i,j,errors=0;
   matrix matrix_a(size_m,size_m);
//--- 填充平方矩阵
   MatrixTestFirst(matrix_a);
//--- 将测量单位微秒
   ulong t1=GetMicrosecondCount();
//--- 求逆矩阵
   matrix inverse=matrix_a.Inv();
//--- 测量
   ulong t2=GetMicrosecondCount();
//--- 检查正确性
   matrix identity=matrix_a.MatMul(inverse);
//---
   for(i=0; i<size_m; i++)
     {
      for(j=0; j<size_m; j++)
        {
         double value;
         //--- 必须沿着对角线填充一
         if(i==j)
            value=1.0;
         else
            value=0.0;
         if(MathClassify(identity[i][j])>FP_ZERO)
            errors++;
         else
           {
            if(identity[i][j]!=value)
              {
               double diff=MathAbs(identity[i][j]-value);
               //--- 乘法和偏差过多，因此降低了检查精度
               if(diff>1e-9)
                  errors++;
              }
           }
        }
     }
//---
   double elapsed_time=double(t2-t1)/1000.0;
   printf("Inversion of matrix %d x %d  %s  errors=%d  time=%.3f ms",size_m,size_m,errors==0?"passed":"failed",errors,elapsed_time);
   return(errors);
  }

7.9.4 PInv

通过摩尔-彭罗斯（Moore-Penrose）方法计算矩阵的伪逆。

matrix matrix::PInv()

返回值

矩阵的伪逆。

举例

int TestPseudoInverse(const int size_m, const int size_k)
  {
   matrix matrix_a(size_m,size_k);
   matrix matrix_inverted(size_k,size_m);
   matrix matrix_temp;
   matrix matrix_a2;
//--- 填充矩阵
   MatrixTestFirst(matrix_a);
//--- invert
   matrix_inverted=matrix_a.PInv();
//--- 检查正确性
   int errors=0;
//--- A * A+ * A = A   (A+ is a pseudo-inverse of A)
   matrix_temp=matrix_a.MatMul(matrix_inverted);
   matrix_a2=matrix_temp.MatMul(matrix_a);
   errors=(int)matrix_a.CompareByDigits(matrix_a2,10);
 
   printf("PseudoInversion %s matrix_size  %d x %d  errors=%d",errors==0?"passed":"failed",size_m,size_k,errors);
//---
   return(errors);
  }

7.10 机器学习

这些方法用于机器学习。

神经网络激活函数根据输入的加权累加和来判定神经元的输出值。 激活函数的选择对神经网络性能有很大影响。 模型部件（层）不同可选用不同的激活函数。

除了所有已知的激活函数外，MQL5 还提供其衍生函数。 函数导数能够根据学习中接到的误差有效地更新模型参数。

神经网络旨在找到一种算法，将学习误差最小化，为此选用了损失函数。 损失函数的值表示模型预测值与实际值的偏差度。 根据问题采用不同的损失函数。 例如，均方误差（MSE） 用于回归问题；二元交叉熵（BCE）用于二元分类目的。

函数	动作
Activation	计算激活函数值，并将其写入传递的向量/矩阵
Derivative	计算激活函数导数值，并将其写入所传递的向量/矩阵
Loss	计算损失函数值，并将其写入所传递的向量/矩阵
LossGradient	计算亏损函数梯度的向量或矩阵
RegressionMetric	在指定数据数组上构建回归线，并计算回归量程作为偏差误差
ConfusionMatrix	计算混淆矩阵。该方法应用于预测值向量
ConfusionMatrixMultilabel	计算每个标签的混淆矩阵。该方法应用于预测值向量
ClassificationMetric	计算分类指标来评估预测数据相对于真实数据的质量。该方法适用于预测值的向量
ClassificationScore	计算分类指标来评估预测数据相对于真实数据的质量
PrecisionRecall	计算值以构建精确调用曲线。与ClassificationScore类似，此方法应用于真值向量
ReceiverOperatingCharacteristic	计算值以构建接收器工作特性(ROC)曲线。与ClassificationScore类似，此方法应用于真值向量

举例

此示例演示如何选用矩阵运算训练模型。 训练的模型针对函数 (a + b + c)^2 / (a^2 + b^2 + c^2)。 我们输入初始数据矩阵，其中 a、b 和 c 包含在不同的列中。 函数结果在模型输出端获得。

matrix weights1, weights2, weights3;               // 权重矩阵
matrix output1, output2, result;                   // 神经层输出矩阵
input int layer1 = 200;                            // 第一个隐藏层的大小
input int layer2 = 200;                            // 第二个隐藏层的大小
input int Epochs = 20000;                          // 训练世代的数量
input double lr = 3e-6;                            // 学习率
input ENUM_ACTIVATION_FUNCTION ac_func = AF_SWISH; // 激活函数
//+------------------------------------------------------------------+
//| 脚本程序 start 函数                                                |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int train = 1000;    // 训练样本大小
   int test = 10;       // 测试样本大小
   matrix m_data, m_target;
//--- 生成训练样本
   if(!CreateData(m_data, m_target, train))  
      return;
//--- 训练模型
   if(!Train(m_data, m_target, Epochs))      
      return;
//--- 生成测试样本
   if(!CreateData(m_data, m_target, test))   
      return;
//--- 测试模型
   Test(m_data, m_target);                   
  }
//+------------------------------------------------------------------+
//| 样本生成方法                                                       |
//+------------------------------------------------------------------+
bool CreateData(matrix &data, matrix &target, const int count)
  {
//--- 初始化初始数据和结果矩阵
   if(!data.Init(count, 3) || !target.Init(count, 1))
      return false;
//--- 用随机值填充初始数据矩阵
   data.Random(-10, 10);                     
//--- 计算训练样本的目标值
   vector X1 = MathPow(data.Col(0) + data.Col(1) + data.Col(1), 2);
   vector X2 = MathPow(data.Col(0), 2) + MathPow(data.Col(1), 2) + MathPow(data.Col(2), 2);
   if(!target.Col(X1 / X2, 0))
      return false;
//--- 返回结果
   return true;
  }
//+------------------------------------------------------------------+
//| 模型训练方法                                                       |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs = 10000)
  {
//--- 创建模型
   if(!CreateNet())
      return false;
//--- 训练模型
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- 前向验算
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, result.Loss(target, LOSS_MSE));
      //--- 权重矩阵的反向传播与更新
      if(!Backprop(data, target))
         return false;
     }
//--- 返回结果
   return true;
  }
//+------------------------------------------------------------------+
//| 模型创建方法                                                       |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- 初始化权重矩阵
   if(!weights1.Init(4, layer1) || !weights2.Init(layer1 + 1, layer2) || !weights3.Init(layer2 + 1, 1))
      return false;
//--- 用随机值填充权重矩阵
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   weights3.Random(-0.1, 0.1);
//--- 返回结果
   return true;
  }
//+------------------------------------------------------------------+
//| 前向验算方法                                                       |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  {
//--- 检查初始数据大小
   if(data.Cols() != weights1.Rows() - 1)
      return false;
//--- 计算第一个神经层
   matrix temp = data;
   if(!temp.Resize(temp.Rows(), weights1.Rows()) ||
      !temp.Col(vector::Ones(temp.Rows()), weights1.Rows() - 1))
      return false;
   output1 = temp.MatMul(weights1);
//--- 计算激活函数
   if(!output1.Activation(temp, ac_func))
      return false;
//--- 计算第二个神经层
   if(!temp.Resize(temp.Rows(), weights2.Rows()) ||
      !temp.Col(vector::Ones(temp.Rows()), weights2.Rows() - 1))
      return false;
   output2 = temp.MatMul(weights2);
//--- 计算激活函数
   if(!output2.Activation(temp, ac_func))
      return false;
//--- 计算第三个神经层
   if(!temp.Resize(temp.Rows(), weights3.Rows()) ||
      !temp.Col(vector::Ones(temp.Rows()), weights3.Rows() - 1))
      return false;
   result = temp.MatMul(weights3);
//--- 返回结果
   return true;
  }
//+------------------------------------------------------------------+
//| 反向传播法                                                         |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- 检查目标值矩阵的大小
   if(target.Rows() != result.Rows() ||
      target.Cols() != result.Cols())
      return false;
//--- 检测计算值与目标的偏差
   matrix loss = (target - result) * 2;
//--- 将梯度传播到上一层
   matrix gradient = loss.MatMul(weights3.Transpose());
//--- 更新最后一层的权重矩阵
   matrix temp;
   if(!output2.Activation(temp, ac_func))
      return false;
   if(!temp.Resize(temp.Rows(), weights3.Rows()) ||
      !temp.Col(vector::Ones(temp.Rows()), weights3.Rows() - 1))
      return false;
   weights3 = weights3 + temp.Transpose().MatMul(loss) * lr;
//--- 依据激活函数的导数调整误差梯度
   if(!output2.Derivative(temp, ac_func))
      return false;
   if(!gradient.Resize(gradient.Rows(), gradient.Cols() - 1))
      return false;
   loss = gradient * temp;
//--- 将梯度传播到更低一层
   gradient = loss.MatMul(weights2.Transpose());
//--- 更新第二隐藏层的权重矩阵
   if(!output1.Activation(temp, ac_func))
      return false;
   if(!temp.Resize(temp.Rows(), weights2.Rows()) ||
      !temp.Col(vector::Ones(temp.Rows()), weights2.Rows() - 1))
      return false;
   weights2 = weights2 + temp.Transpose().MatMul(loss) * lr;
//--- 依据激活函数的导数调整误差梯度
   if(!output1.Derivative(temp, ac_func))
      return false;
   if(!gradient.Resize(gradient.Rows(), gradient.Cols() - 1))
      return false;
   loss = gradient * temp;
//--- 更新第一隐藏层的权重矩阵
   temp = data;
   if(!temp.Resize(temp.Rows(), weights1.Rows()) ||
      !temp.Col(vector::Ones(temp.Rows()), weights1.Rows() - 1))
      return false;
   weights1 = weights1 + temp.Transpose().MatMul(loss) * lr;
//--- 返回结果
   return true;
  }
//+------------------------------------------------------------------+
//| 模型测试方法                                                       |
//+------------------------------------------------------------------+
bool Test(matrix &data, matrix &target)
  {
//--- 前向测试数据
   if(!FeedForward(data))
      return false;
//--- 记录模型计算结果和真实值
   PrintFormat("Test loss %.5f", result.Loss(target, LOSS_MSE));
   ulong total = data.Rows();
   for(ulong i = 0; i < total; i++)
      PrintFormat("(%.2f + %.2f + %.2f)^2 / (%.2f^2 + %.2f^2 + %.2f^2) =  Net %.2f, Target %.2f", data[i, 0], data[i, 1], data[i, 2],
                  data[i, 0], data[i, 1], data[i, 2], result[i, 0], target[i, 0]);
//--- 返回结果
   return true;
  }
//+------------------------------------------------------------------+

7.10.1 Activation

计算激活函数值，并将其写入传递的向量/矩阵。

bool vector::Activation(
  vector&                   vect_out,      // 获取函数值的向量
  ENUM_ACTIVATION_FUNCTION  activation,    // 激活函数
   ...                                     // 附加参数
   );
 
 
bool matrix::Activation(
  matrix&                   matrix_out,    // 获取函数值的矩阵
  ENUM_ACTIVATION_FUNCTION  activation     // 激活函数
   );
 
 
bool matrix::Activation(
  matrix&                   matrix_out,    // 获取函数值的矩阵
  ENUM_ACTIVATION_FUNCTION  activation,    // 激活函数
  ENUM_MATRIX_AXIS          axis,          // 轴线
   ...                                     // 附加参数
   );

参数

vect_out/matrix_out

[out] 获取激活函数计算值的向量或矩阵。

activation

[in] ENUM_ACTIVATION_FUNCTION枚举中的激活函数。

axis

[in] ENUM_MATRIX_AXIS枚举值（AXIS_HORZ ― 横轴，AXIS_VERT ― 竖轴）。

...

[in] 某些激活函数所需的附加参数。如果没有指定参数，则使用默认值。

返回值

如果成功返回true，否则返回false。

附加参数

某些激活函数接受附加参数。如果没有指定参数，则使用默认值

   AF_ELU  (Exponential Linear Unit)  
     double alpha=1.0
   
   Activation function: if(x>=0) f(x) = x
                      else f(x) = alpha * (exp(x)-1)
   
   
   AF_LINEAR   
     double alpha=1.0
     double beta=0.0
   
   Activation function: f(x) = alpha*x + beta
   
   
   AF_LRELU   (Leaky REctified Linear Unit)   
     double alpha=0.3
   
   Activation function: if(x>=0) f(x)=x
                      else f(x) = alpha*x
   
                        
   AF_RELU  (REctified Linear Unit)   
     double alpha=0.0
     double max_value=0.0
     double treshold=0.0
   
   Activation function: if(alpha==0) f(x) = max(x,0)
                      else if(x>max_value) f(x) = x
                      else f(x) = alpha*(x - treshold)
   
   
   AF_SWISH   
     double beta=1.0
   
   Activation function: f(x) = x / (1+exp(-x*beta))
   
   
   AF_TRELU   (Thresholded REctified Linear Unit)   
     double theta=1.0
   
   Activation function: if(x>theta) f(x) = x
                      else f(x) = 0
   
   
   AF_PRELU   (Parametric REctified Linear Unit)   
     double alpha[] - learned array of coeefficients
   
   Activation function: if(x[i]>=0) f(x)[i] = x[i]
                      else f(x)[i] = alpha[i] * x[i]

注意

在人工神经网络中，神经元的激活函数决定输出信号，输出信号由一个输入信号或一组输入信号定义。激活函数的选择对神经网络的性能有很大的影响。不同的模型部件(层)可以使用不同的激活函数。

使用附加参数的示例：

   vector x={0.1, 0.4, 0.9, 2.0, -5.0, 0.0, -0.1};
   vector y;
 
   x.Activation(y,AF_ELU);
   Print(y);
   x.Activation(y,AF_ELU,2.0);
   Print(y);
 
   Print("");
   x.Activation(y,AF_LINEAR);
   Print(y);
   x.Activation(y,AF_LINEAR,2.0);
   Print(y);
   x.Activation(y,AF_LINEAR,2.0,5.0);
   Print(y);
 
   Print("");
   x.Activation(y,AF_LRELU);
   Print(y);
   x.Activation(y,AF_LRELU,1.0);
   Print(y);
   x.Activation(y,AF_LRELU,0.1);
   Print(y);
  
   Print("");
   x.Activation(y,AF_RELU);
   Print(y);
   x.Activation(y,AF_RELU,2.0,0.5);
   Print(y);
   x.Activation(y,AF_RELU,2.0,0.5,1.0);
   Print(y);
 
   Print("");
   x.Activation(y,AF_SWISH);
   Print(y);
   x.Activation(y,AF_SWISH,2.0);
   Print(y);
 
   Print("");
   x.Activation(y,AF_TRELU);
   Print(y);
   x.Activation(y,AF_TRELU,0.3);
   Print(y);
 
   Print("");
   vector a=vector::Full(x.Size(),2.0);
   x.Activation(y,AF_PRELU,a);
   Print(y);
 
/*  Results
   [0.1,0.4,0.9,2,-0.993262053000915,0,-0.095162581964040]
   [0.1,0.4,0.9,2,-1.986524106001829,0,-0.190325163928081]
   
   [0.1,0.4,0.9,2,-5,0,-0.1]
   [0.2,0.8,1.8,4,-10,0,-0.2]
   [5.2,5.8,6.8,9,-5,5,4.8]
   
   [0.1,0.4,0.9,2,-1.5,0,-0.03]
   [0.1,0.4,0.9,2,-5,0,-0.1]
   [0.1,0.4,0.9,2,-0.5,0,-0.01]
   
   [0.1,0.4,0.9,2,0,0,0]
   [0.2,0.8,0.9,2,-10,0,-0.2]
   [-1.8,-1.2,0.9,2,-12,-2,-2.2]
   
   [0.052497918747894,0.239475064044981,0.6398545523625035,1.761594155955765,-0.03346425462142428,0,-0.047502081252106]
   [0.054983399731247,0.275989792451045,0.7723340415895611,1.964027580075817,-0.00022698934351217,0,-0.045016600268752]
   
   [0,0,0,2,0,0,0]
   [0,0.4,0.9,2,0,0,0]
   
   [0.1,0.4,0.9,2,-10,0,-0.2]
*/

7.10.2 Derivative

计算激活函数的导数值，并将其写入传递的向量/矩阵。

bool vector::Derivative(
  vector&                   vect_out,      // 获取函数值的向量
  ENUM_ACTIVATION_FUNCTION  activation,    // 激活函数
   ...                                     // 附加参数
   );
 
 
bool matrix::Derivative(
  matrix&                   matrix_out,    // 获取函数值的矩阵
  ENUM_ACTIVATION_FUNCTION  activation,    // 激活函数
   );
 
 
bool matrix::Derivative(
  matrix&                   matrix_out,    // 获取函数值的矩阵
  ENUM_ACTIVATION_FUNCTION  activation,    // 激活函数
  ENUM_MATRIX_AXIS          axis,          // 轴线
   ...                                     // 附加参数
   );

参数

vect_out/matrix_out

[out] 获取激活函数导数计算值的向量或矩阵。

activation

[in] ENUM_ACTIVATION_FUNCTION枚举中的激活函数。

axis

[in] ENUM_MATRIX_AXIS枚举值（AXIS_HORZ ― 横轴，AXIS_VERT ― 竖轴）。

...

[in] 附加参数与激活函数的参数相同。只有某些激活函数接受附加参数。如果没有指定参数，则使用默认值。

返回值

如果成功返回true，否则返回false。

注意

在误差反向传播过程中，函数导数能够基于学习过程中接收到的误差有效地更新模型参数。

7.10.3 Loss

计算损失函数的值。

double vector::Loss(
  const vector&       vect_true,     // 真值向量
  ENUM_LOSS_FUNCTION  loss,          // 损失函数
   ...                               // 附加参数
   );
 
 
double matrix::Loss(
  const matrix&       matrix_true,   // 真值矩阵
  ENUM_LOSS_FUNCTION  loss,          // 损失函数
   );
 
 
double matrix::Loss(
  const matrix&       matrix_true,   // 真值矩阵
  ENUM_LOSS_FUNCTION  loss,          // 损失函数
  ENUM_MATRIX_AXIS    axis,          // 轴线
   ...                               // 附加参数
   );

参数

vect_true/matrix_true

[in] 真值的向量或矩阵。

loss

[in] ENUM_LOSS_FUNCTION枚举中的损失函数。

axis

[in] ENUM_MATRIX_AXIS枚举值（AXIS_HORZ ― 横轴，AXIS_VERT ― 竖轴）。

...

[in] 附加参数'delta'只能由Hubert损失函数(LOSS_HUBER)使用

返回值

双数值。

如果Hubert损失函数(LOSS_HUBER)中使用在'delta'参数

   double delta = 1.0;
   double error = fabs(y - x);
   if(error<delta)
      loss = 0.5 * error^2;
   else
      loss = 0.5 * delta^2 + delta * (error - delta);

注意

神经网络的目标是找到最小化训练样本误差的算法，为此使用损失函数。

损失函数的值表示模型预测值与实际值偏差的程度。

根据不同的问题使用不同的损失函数。例如，均方误差(MSE)用于回归问题，二元交叉熵(BCE)用于二元分类。

调用Hubert损失函数的示例：

   vector y_true = {0.0, 1.0, 0.0, 0.0};
   vector y_pred = {0.6, 0.4, 0.4, 0.6};
   double loss=y_pred.Loss(y_true,LOSS_HUBER);
   Print(loss);
   double loss2=y_pred.Loss(y_true,LOSS_HUBER,0.5);
   Print(loss2);
 
/* Result
   0.155
   0.15125
*/

7.10.4 LossGradient

计算损失函数梯度的向量或矩阵。

vector vector::LossGradient(
  const vector&       vect_true,     // 真值向量
  ENUM_LOSS_FUNCTION  loss,          // 损失函数类型
   ...                               // 附加参数
   );
 
 
matrix matrix::LossGradient(
  const matrix&       matrix_true,   // 真值矩阵
  ENUM_LOSS_FUNCTION  loss,          // 损失函数
   );
 
 
matrix matrix::LossGradient(
  const matrix&       matrix_true,   // 真值矩阵
  ENUM_LOSS_FUNCTION  loss,          // 损失函数
  ENUM_MATRIX_AXIS    axis,          // 轴线
   ...                               // 附加参数
   );

参数

vect_true/matrix_true

[in] 真值的向量或矩阵。

loss

[in] ENUM_LOSS_FUNCTION枚举中的损失函数。

axis

[in] ENUM_MATRIX_AXIS枚举值（AXIS_HORZ ― 横轴，AXIS_VERT ― 竖轴）。

...

[in] 附加参数'delta'只能由Hubert损失函数(LOSS_HUBER)使用

返回值

损失函数梯度值的向量或矩阵。梯度是损失函数在给定点上对dx的偏导数（x是预测值）。

注意

神经网络在训练模型时，在反向传播过程中使用梯度来调整权重矩阵的权重。

神经网络的目标是找到最小化训练样本误差的算法，为此使用损失函数。

根据不同的问题使用不同的损失函数。例如，均方误差(MSE)用于回归问题，二元交叉熵(BCE)用于二元分类。

计算损失函数梯度的示例

   matrixf y_true={{ 1, 2, 3, 4 },
                   { 5, 6, 7, 8 },
                   { 9,10,11,12 }};
   matrixf y_pred={{ 1, 2, 3, 4 },
                   {11,10, 9, 8 },
                   { 5, 6, 7,12 }};
   matrixf loss_gradient =y_pred.LossGradient(y_true,LOSS_MAE);
   matrixf loss_gradienth=y_pred.LossGradient(y_true,LOSS_MAE,AXIS_HORZ);
   matrixf loss_gradientv=y_pred.LossGradient(y_true,LOSS_MAE,AXIS_VERT);
   Print("loss gradients\n",loss_gradient);
   Print("loss gradients on horizontal axis\n",loss_gradienth);
   Print("loss gradients on vertical axis\n",loss_gradientv);
 
/* Result
   loss gradients
   [[0,0,0,0]
    [0.083333336,0.083333336,0.083333336,0]
    [-0.083333336,-0.083333336,-0.083333336,0]]
   loss gradients on horizontal axis
   [[0,0,0,0]
    [0.33333334,0.33333334,0.33333334,0]
    [-0.33333334,-0.33333334,-0.33333334,0]]
   loss gradients on vertical axis
   [[0,0,0,0]
    [0.25,0.25,0.25,0]
    [-0.25,-0.25,-0.25,0]]
*/

7.10.5 RegressionMetric

计算回归指标来评估预测数据与真实数据相比的质量

double vector::RegressionMetric(
   const vector&           vector_true,   // 真值向量
   ENUM_REGRESSION_METRIC  metric         // 指标类型
   );
 
double matrix::RegressionMetric(
   const matrix&           matrix_true,   // 真值矩阵
   ENUM_REGRESSION_METRIC  metric         // 指标类型
);
 
vector matrix::RegressionMetric(
   const matrix&           matrix_true,   // 真值矩阵
   ENUM_REGRESSION_METRIC  metric,        // 指标类型
   int                     axis           // 轴线
   );

参数

vector_true/matrix_true

[in] 真值的向量或矩阵。

metric

[in] 来自ENUM_REGRESSION_METRIC枚举的指标类型。

axis

[in] 轴线。0 ― 横轴，1 ― 竖轴。

返回值

计算用于评估预测数据与真实数据相比的质量的指标

注意

REGRESSION_MAE ― 平均绝对误差，表示预测值与相应真值之间的绝对差值 REGRESSION_MSE ― 均方误差，表示预测值与对应真值之间的平方差 REGRESSION_RMSE ― 均方根误差(RMSE) REGRESSION_R2 - 1 ― MSE（回归）/ MSE（平均） REGRESSION_MAPE ― 平均绝对误差(MAE)百分比 REGRESSION_MSPE ― 均方误差(MSE)百分比 REGRESSION_RMSLE ― 按对数尺计算的RMSE（均方根误差）

例如：

   vector y_true = {3, -0.5, 2, 7};
   vector y_pred = {2.5, 0.0, 2, 8};
//---
   double mse=y_pred.RegressionMetric(y_true,REGRESSION_MSE);
   Print("mse=",mse);
//---
   double mae=y_pred.RegressionMetric(y_true,REGRESSION_MAE);
   Print("mae=",mae);
//---
   double r2=y_pred.RegressionMetric(y_true,REGRESSION_R2);
   Print("r2=",r2);
 
  /* Result
   mae=0.375
   mse=0.5
   r2=0.9486081370449679
   */

7.10.6 ConfusionMatrix

计算混淆矩阵。该方法应用于预测值向量。

matrix vector::ConfusionMatrix(
   const vector&       vect_true      // 真值向量
   );
 
 
matrix vector::ConfusionMatrix(
   const vector&       vect_true,     // 真值向量
   uint                label          //选项卡值
   );

参数

vect_true

[in] 真值向量。

label

[in] 计算混淆矩阵的标签值。

返回值

混淆矩阵。如果未指定标签值，则返回多类混淆矩阵，其中每个标签单独与其他标签匹配。如果指定了标签值，则返回一个2 x 2矩阵，其中指定的标签被视为正数，而所有其他标签均为负数（ovr，一vs其余）。

注意

混淆矩阵C使得Cij等于已知属于组i且预测属于组j的观察值的数量。因此，在二元分类中，真阴性(TN)的计数为C00，假阴性(FN)为C10，真阳性(TP)为C11，假阳性(FP)为C01。

换句话说，矩阵可以用图形表示如下：

TN	FP
FN	TP

真实值向量和预测值向量的大小应该相同。

示例：

   vector y_true={7,2,1,0,4,1,4,9,5,9,0,6,9,0,1,5,9,7,3,4,8,4,2,7,6,8,4,2,3,6};
   vector y_pred={7,2,1,0,4,1,4,9,5,9,0,6,9,0,1,5,9,7,3,4,2,9,4,9,5,9,2,7,7,0};
   matrix confusion=y_pred.ConfusionMatrix(y_true);
   Print(confusion);
   confusion=y_pred.ConfusionMatrix(y_true,0);
   Print(confusion);
   confusion=y_pred.ConfusionMatrix(y_true,1);
   Print(confusion);
   confusion=y_pred.ConfusionMatrix(y_true,2);
   Print(confusion);
 
 
/*
  [[3,0,0,0,0,0,0,0,0,0]
   [0,3,0,0,0,0,0,0,0,0]
   [0,0,1,0,1,0,0,1,0,0]
   [0,0,0,1,0,0,0,1,0,0]
   [0,0,1,0,3,0,0,0,0,1]
   [0,0,0,0,0,2,0,0,0,0]
   [1,0,0,0,0,1,1,0,0,0]
   [0,0,0,0,0,0,0,2,0,1]
   [0,0,1,0,0,0,0,0,0,1]
   [0,0,0,0,0,0,0,0,0,4]]
  [[26,1]
   [0,3]]
  [[27,0]
   [0,3]]
  [[25,2]
   [2,1]]
*/

7.10.7 ConfusionMatrixMultilabel

计算每个标签的混淆矩阵。该方法应用于预测值向量。

uint vector::ConfusionMatrixMultiLabel(
   const vector&       vect_true,     // 真值向量
   matrix&             confusions[]   // 计算混淆矩阵的数组 
   );

参数

vect_true

[in] 真值向量。

confusions

[out] 一个2 × 2矩阵数组，为每个标签计算混淆矩阵。

返回值

计算的混淆矩阵数组的大小。如果失败，则返回0

注意

结果数组可以是动态也可以是静态。如果是静态数组，那么其大小必须不小于类的数量。

真实值向量和预测值向量的大小应该相同。

示例：

   vector y_true={7,2,1,0,4,1,4,9,5,9,0,6,9,0,1,5,9,7,3,4,8,4,2,7,6,8,4,2,3,6};
   vector y_pred={7,2,1,0,4,1,4,9,5,9,0,6,9,0,1,5,9,7,3,4,2,9,4,9,5,9,2,7,7,0};
   matrix label_confusions[12];
 
   uint   res=y_pred.ConfusionMatrixMultiLabel(y_true,label_confusions);
   Print("res=",res,"  size=",label_confusions.Size());
   for(uint i=0; i<res; i++)
      Print(label_confusions[i]);
 
 
/*
  res=10  size=12
  [[26,1]
   [0,3]]
  [[27,0]
   [0,3]]
  [[25,2]
   [2,1]]
  [[28,0]
   [1,1]]
  [[24,1]
   [2,3]]
  [[27,1]
   [0,2]]
  [[27,0]
   [2,1]]
  [[25,2]
   [1,2]]
  [[28,0]
   [2,0]]
  [[23,3]
   [0,4]]
*/

7.10.8 ClassificationMetric

计算分类指标来评估预测数据相对于真实数据的质量。该方法适用于预测值的向量。

vector vector::ClassificationMetric(
   const vector&              vect_true,     // 真值向量
   ENUM_CLASSIFICATION_METRIC metric         // 指标类型
   );
 
 
vector vector::ClassificationMetric(
   const vector&              vect_true,     // 真值向量
   ENUM_CLASSIFICATION_METRIC metric         // 指标类型
   ENUM_AVERAGE_MODE          mode           // 平均模式
   );

参数

vect_true

[in] 真值向量。

metric

[in] ENUM_CLASSIFICATION_METRIC枚举的指标类型。应用CLASSIFICATION_TOP_K_ACCURACY， CLASSIFICATION_AVERAGE_PRECISION和CLASSIFICATION_ROC_AUC（在ClassificationScore方法中使用）以外的值。

mode

[in] ENUM_AVERAGE_MODE枚举的平均模式。用于CLASSIFICATION_F1，CLASSIFICATION_JACCARD， CLASSIFICATION_PRECISION和CLASSIFICATION_RECALL指标。

返回值

包含计算指标的向量。在AVERAGE_NONE平均模式的情况下，向量包含每个类别的指标值，而不进行平均。（例如，在二元分类的情况下，这将是分别用于'false'和'true'的两个指标）。

关于平均模式的说明

AVERAGE_BINARY只对二元分类有意义。

AVERAGE_MICRO ― 通过计算真阳性、假阴性和假阳性总数来计算全局指标。

AVERAGE_MACRO ― 计算每个标签的指标并找到其未加权平均值。这没有考虑标签不平衡。

AVERAGE_WEIGHTED ― 计算每个标签的指标并找到其按支持度加权的平均值（每个标签的真实实例数）。这改变了‘macro’以解决标签不平衡的问题；它可能会导致不在精确率和召回率之间的F分数。

示例：

   vector y_true={7,2,1,0,4,1,4,9,5,9,0,6,9,0,1,5,9,7,3,4,8,4,2,7,6,8,4,2,3,6};
   vector y_pred={7,2,1,0,4,1,4,9,5,9,0,6,9,0,1,5,9,7,3,4,2,9,4,9,5,9,2,7,7,0};
 
   vector accuracy=y_pred.ClassificationMetric(y_true,CLASSIFICATION_ACCURACY);
   Print("accuracy=",accuracy);
   vector balanced=y_pred.ClassificationMetric(y_true,CLASSIFICATION_BALANCED_ACCURACY);
   Print("balanced=",balanced);
   Print("");
 
   vector f1_micro=y_pred.ClassificationMetric(y_true,CLASSIFICATION_F1,AVERAGE_MICRO);
   Print("f1_micro=",f1_micro);
   vector f1_macro=y_pred.ClassificationMetric(y_true,CLASSIFICATION_F1,AVERAGE_MACRO);
   Print("f1_macro=",f1_macro);
   vector f1_weighted=y_pred.ClassificationMetric(y_true,CLASSIFICATION_F1,AVERAGE_WEIGHTED);
   Print("f1_weighted=",f1_weighted);
   vector f1_none=y_pred.ClassificationMetric(y_true,CLASSIFICATION_F1,AVERAGE_NONE);
   Print("f1_none=",f1_none);
   Print("");
 
   vector jaccard_micro=y_pred.ClassificationMetric(y_true,CLASSIFICATION_JACCARD,AVERAGE_MICRO);
   Print("jaccard_micro=",jaccard_micro);
   vector jaccard_macro=y_pred.ClassificationMetric(y_true,CLASSIFICATION_JACCARD,AVERAGE_MACRO);
   Print("jaccard_macro=",jaccard_macro);
   vector jaccard_weighted=y_pred.ClassificationMetric(y_true,CLASSIFICATION_JACCARD,AVERAGE_WEIGHTED);
   Print("jaccard_weighted=",jaccard_weighted);
   vector jaccard_none=y_pred.ClassificationMetric(y_true,CLASSIFICATION_JACCARD,AVERAGE_NONE);
   Print("jaccard_none=",jaccard_none);
   Print("");
 
   vector precision_micro=y_pred.ClassificationMetric(y_true,CLASSIFICATION_PRECISION,AVERAGE_MICRO);
   Print("precision_micro=",precision_micro);
   vector precision_macro=y_pred.ClassificationMetric(y_true,CLASSIFICATION_PRECISION,AVERAGE_MACRO);
   Print("precision_macro=",precision_macro);
   vector precision_weighted=y_pred.ClassificationMetric(y_true,CLASSIFICATION_PRECISION,AVERAGE_WEIGHTED);
   Print("precision_weighted=",precision_weighted);
   vector precision_none=y_pred.ClassificationMetric(y_true,CLASSIFICATION_PRECISION,AVERAGE_NONE);
   Print("precision_none=",precision_none);
   Print("");
 
   vector recall_micro=y_pred.ClassificationMetric(y_true,CLASSIFICATION_RECALL,AVERAGE_MICRO);
   Print("recall_micro=",recall_micro);
   vector recall_macro=y_pred.ClassificationMetric(y_true,CLASSIFICATION_RECALL,AVERAGE_MACRO);
   Print("recall_macro=",recall_macro);
   vector recall_weighted=y_pred.ClassificationMetric(y_true,CLASSIFICATION_RECALL,AVERAGE_WEIGHTED);
   Print("recall_weighted=",recall_weighted);
   vector recall_none=y_pred.ClassificationMetric(y_true,CLASSIFICATION_RECALL,AVERAGE_NONE);
   Print("recall_none=",recall_none);
   Print("");
 
//--- 二元分类
   vector y_pred_bin={0,1,0,1,1,0,0,0,1};
   vector y_true_bin={1,0,0,0,1,0,1,1,1};
 
   vector f1_bin=y_pred_bin.ClassificationMetric(y_true_bin,CLASSIFICATION_F1,AVERAGE_BINARY);
   Print("f1_bin=",f1_bin);
   vector jaccard_bin=y_pred_bin.ClassificationMetric(y_true_bin,CLASSIFICATION_JACCARD,AVERAGE_BINARY);
   Print("jaccard_bin=",jaccard_bin);
   vector precision_bin=y_pred_bin.ClassificationMetric(y_true_bin,CLASSIFICATION_PRECISION,AVERAGE_BINARY);
   Print("precision_bin=",precision_bin);
   vector recall_bin=y_pred_bin.ClassificationMetric(y_true_bin,CLASSIFICATION_RECALL,AVERAGE_BINARY);
   Print("recall_bin=",recall_bin);
 
 
/*
  accuracy=[0.6666666666666666]
  balanced=[0.6433333333333333]
  
  f1_micro=[0.6666666666666666]
  f1_macro=[0.6122510822510823]
  f1_weighted=[0.632049062049062]
  f1_none=[0.8571428571428571,1,0.3333333333333333,0.6666666666666666,0.6666666666666665,0.8,0.5,0.5714285714285715,0,0.7272727272727273]
  
  jaccard_micro=[0.5]
  jaccard_macro=[0.4921428571428572]
  jaccard_weighted=[0.5056349206349205]
  jaccard_none=[0.75,1,0.2,0.5,0.5,0.6666666666666666,0.3333333333333333,0.4,0,0.5714285714285714]
  
  precision_micro=[0.6666666666666666]
  precision_macro=[0.6571428571428571]
  precision_weighted=[0.6706349206349207]
  precision_none=[0.75,1,0.3333333333333333,1,0.75,0.6666666666666666,1,0.5,0,0.5714285714285714]
  
  recall_micro=[0.6666666666666666]
  recall_macro=[0.6433333333333333]
  recall_weighted=[0.6666666666666666]
  recall_none=[1,1,0.3333333333333333,0.5,0.6,1,0.3333333333333333,0.6666666666666666,0,1]
  
  f1_bin=[0.4444444444444445]
  jaccard_bin=[0.2857142857142857]
  precision_bin=[0.5]
  recall_bin=[0.4]
*/

7.10.9 ClassificationScore

计算分类指标来评估预测数据相对于真实数据的质量。

与机器学习部分中的其他方法不同，这个指标适用于真实值的向量，而不是预测值的向量。

vector vector::ClassificationScore(
   const matrix&              pred_scores,   // 包含每一类概率分布的矩阵 
   ENUM_CLASSIFICATION_METRIC metric         // 指标类型
   ENUM_AVERAGE_MODE          mode           // 平均模式
   );
 
 
vector vector::ClassificationScore(
   const matrix&              pred_scores,   // 包含每一类概率分布的矩阵 
   ENUM_CLASSIFICATION_METRIC metric         // 指标类型
   int                        param          // 附加参数
   );

参数

pred_scores

[in] 包含一组水平向量和每一类概率的矩阵。矩阵行数应与真值向量的大小相对应。

metric

[in] ENUM_CLASSIFICATION_METRIC枚举的指标类型。使用CLASSIFICATION_TOP_K_ACCURACY， CLASSIFICATION_AVERAGE_PRECISION和CLASSIFICATION_ROC_AUC值。

mode

[in] ENUM_AVERAGE_MODE枚举的平均模式。用于CLASSIFICATION_AVERAGE_PRECISION和CLASSIFICATION_ROC_AUC指标。

param

[in] 对于CLASSIFICATION_TOP_K_ACCURACY指标，应指定整数K值来替代平均模式。

返回值

包含计算指标的向量。在AVERAGE_NONE平均模式的情况下，向量包含每个类别的指标值，而不进行平均。（例如，在二元分类的情况下，这将是分别用于'false'和'true'的两个指标）。

关于平均模式的说明

AVERAGE_BINARY只对二元分类有意义。

AVERAGE_MICRO ― 通过将标签指标矩阵的每个元素视为一个标签来计算全局指标。标签指标矩阵是指一个矩阵，其中包含每个标签的一组概率。

AVERAGE_MACRO ― 计算每个标签的指标并找到其未加权平均值。这没有考虑标签不平衡。

AVERAGE_WEIGHTED ― 计算每个标签的指标并找到其按支持度加权的平均值（每个标签的真实实例数）。

注意

在二元分类的情况下，我们不仅可以输入一个n x 2矩阵，其中第一列包含负标签的概率，第二列包含正标签的概率，还可以输入一个由一列正概率组成的矩阵。这是因为二元分类模型可以返回正标签的两个概率或一个概率。

示例：

   vector y_true={7,2,1,0,4,1,4,9,5,9,0,6,9,0,1,5,9,7,3,4,8,4,2,7,6,8,4,2,3,6};
   //vector y_pred={7,2,1,0,4,1,4,9,5,9,0,6,9,0,1,5,9,7,3,4,2,9,4,9,5,9,2,7,7,0};
 
//--- label scores          0         1         2         3         4         5         6         7         8         9    true pred
   matrix y_scores={{0.000109, 0.000186, 0.000449, 0.000052, 0.000002, 0.000022, 0.000005, 0.998059, 0.000010, 0.001104},  // 7    7
                    {0.000091, 0.081956, 0.916816, 0.001106, 0.000006, 0.000002, 0.000001, 0.000000, 0.000021, 0.000000},  // 2    2
                    {0.000108, 0.972863, 0.003600, 0.000021, 0.010479, 0.000015, 0.000131, 0.010385, 0.002339, 0.000060},  // 1    1
                    {0.925425, 0.000080, 0.002913, 0.000057, 0.000274, 0.000638, 0.063529, 0.000316, 0.000095, 0.006673},  // 0    0
                    {0.000060, 0.000126, 0.000006, 0.000000, 0.993513, 0.000000, 0.000003, 0.000222, 0.000001, 0.006069},  // 4    4
                    {0.000016, 0.982124, 0.000045, 0.000002, 0.008445, 0.000001, 0.000005, 0.009230, 0.000120, 0.000013},  // 1    1
                    {0.000000, 0.000040, 0.000001, 0.000000, 0.989395, 0.000167, 0.000004, 0.000070, 0.000177, 0.010146},  // 4    4
                    {0.000795, 0.002938, 0.023447, 0.007418, 0.021838, 0.002476, 0.000260, 0.047551, 0.000082, 0.893194},  // 9    9
                    {0.000091, 0.000226, 0.000038, 0.000007, 0.000048, 0.854910, 0.068644, 0.000080, 0.001097, 0.074860},  // 5    5
                    {0.000000, 0.000000, 0.000000, 0.000000, 0.003004, 0.000000, 0.000000, 0.000035, 0.000000, 0.996960},  // 9    9
                    {0.998856, 0.000009, 0.000976, 0.000002, 0.000000, 0.000013, 0.000131, 0.000006, 0.000000, 0.000007},  // 0    0
                    {0.000178, 0.000446, 0.000326, 0.000033, 0.000193, 0.000071, 0.998403, 0.000015, 0.000328, 0.000007},  // 6    6
                    {0.000005, 0.000016, 0.000153, 0.000045, 0.004110, 0.000012, 0.000015, 0.000031, 0.000076, 0.995537},  // 9    9
                    {0.994188, 0.000003, 0.002584, 0.000005, 0.000005, 0.000100, 0.000739, 0.001473, 0.000038, 0.000864},  // 0    0
                    {0.000173, 0.990569, 0.000792, 0.000040, 0.001798, 0.000035, 0.000114, 0.004750, 0.001716, 0.000013},  // 1    1
                    {0.000000, 0.000537, 0.000008, 0.005080, 0.000046, 0.992910, 0.000012, 0.000671, 0.000390, 0.000347},  // 5    5
                    {0.000127, 0.000003, 0.000003, 0.000000, 0.001583, 0.000000, 0.000002, 0.000555, 0.000016, 0.997712},  // 9    9
                    {0.000001, 0.000012, 0.000072, 0.000020, 0.000000, 0.000000, 0.000000, 0.999868, 0.000000, 0.000026},  // 7    7
                    {0.000020, 0.000105, 0.001139, 0.901343, 0.002132, 0.083873, 0.000124, 0.000097, 0.010981, 0.000186},  // 3    3
                    {0.000002, 0.000048, 0.000019, 0.000000, 0.999347, 0.000002, 0.000040, 0.000051, 0.000000, 0.000489},  // 4    4
                    {0.000059, 0.001344, 0.612502, 0.002749, 0.000229, 0.000678, 0.000038, 0.001844, 0.379727, 0.000831},  // 8    2
                    {0.000586, 0.000740, 0.001625, 0.000007, 0.269341, 0.000076, 0.016417, 0.000199, 0.000107, 0.710902},  // 4    9
                    {0.009547, 0.018055, 0.283795, 0.071079, 0.426074, 0.082335, 0.036379, 0.021188, 0.003924, 0.047623},  // 2    4
                    {0.002506, 0.002545, 0.001148, 0.005659, 0.020416, 0.000112, 0.006092, 0.272536, 0.003148, 0.685839},  // 7    9
                    {0.001263, 0.001769, 0.000293, 0.000011, 0.000302, 0.881768, 0.112019, 0.000125, 0.002327, 0.000123},  // 6    5
                    {0.002904, 0.002909, 0.013421, 0.001461, 0.007519, 0.001251, 0.000555, 0.106219, 0.107125, 0.756637},  // 8    9
                    {0.000055, 0.001080, 0.893158, 0.000000, 0.104492, 0.000159, 0.001042, 0.000013, 0.000000, 0.000000},  // 4    2
                    {0.000344, 0.002693, 0.071184, 0.000262, 0.000001, 0.000003, 0.000032, 0.924362, 0.000714, 0.000404},  // 2    7
                    {0.001404, 0.009375, 0.002638, 0.229189, 0.000064, 0.000896, 0.007516, 0.743557, 0.004462, 0.000897},  // 3    7
                    {0.491140, 0.000125, 0.000024, 0.000302, 0.000038, 0.034947, 0.473161, 0.000170, 0.000028, 0.000066}}; // 6    0
 
   vector top_k=y_true.ClassificationScore(y_scores,CLASSIFICATION_TOP_K_ACCURACY,1);
   Print("top 1 accuracy score = ",top_k);
   top_k=y_true.ClassificationScore(y_scores,CLASSIFICATION_TOP_K_ACCURACY,2);
   Print("top 2 accuracy score = ",top_k);
   vector y_true2={0, 1, 2, 2};
   matrix y_score2={{0.5, 0.2, 0.2},  // 0 is in top 2
                    {0.3, 0.4, 0.2},  // 1 is in top 2
                    {0.2, 0.4, 0.3},  // 2 is in top 2
                    {0.7, 0.2, 0.1}}; // 2 isn't in top 2
   top_k=y_true2.ClassificationScore(y_score2,CLASSIFICATION_TOP_K_ACCURACY,2);
   Print("top k = ",top_k);
   Print("");
 
   vector ap_micro=y_true.ClassificationScore(y_scores,CLASSIFICATION_AVERAGE_PRECISION,AVERAGE_MICRO);
   Print("average precision score micro = ",ap_micro);
   vector ap_macro=y_true.ClassificationScore(y_scores,CLASSIFICATION_AVERAGE_PRECISION,AVERAGE_MACRO);
   Print("average precision score macro = ",ap_macro);
   vector ap_weighted=y_true.ClassificationScore(y_scores,CLASSIFICATION_AVERAGE_PRECISION,AVERAGE_WEIGHTED);
   Print("average precision score weighted = ",ap_weighted);
   vector ap_none=y_true.ClassificationScore(y_scores,CLASSIFICATION_AVERAGE_PRECISION,AVERAGE_NONE);
   Print("average precision score none = ",ap_none);
   Print("");
 
   vector area_micro=y_true.ClassificationScore(y_scores,CLASSIFICATION_ROC_AUC,AVERAGE_MICRO);
   Print("roc auc score micro = ",area_micro);
   vector area_macro=y_true.ClassificationScore(y_scores,CLASSIFICATION_ROC_AUC,AVERAGE_MACRO);
   Print("roc auc score macro = ",area_macro);
   vector area_weighted=y_true.ClassificationScore(y_scores,CLASSIFICATION_ROC_AUC,AVERAGE_WEIGHTED);
   Print("roc auc score weighted = ",area_weighted);
   vector area_none=y_true.ClassificationScore(y_scores,CLASSIFICATION_ROC_AUC,AVERAGE_NONE);
   Print("roc auc score none = ",area_none);
   Print("");
 
//--- 二元分类
   vector y_pred_bin={0,1,0,1,1,0,0,0,1};
   vector y_true_bin={1,0,0,0,1,0,1,1,1};
   vector y_score_true={0.3,0.7,0.1,0.6,0.9,0.0,0.4,0.2,0.8};
   matrix y_score1_bin(y_score_true.Size(),1);
   y_score1_bin.Col(y_score_true,0);
   matrix y_scores_bin={{0.7, 0.3},
                        {0.3, 0.7},
                        {0.9, 0.1},
                        {0.4, 0.6},
                        {0.1, 0.9},
                        {1.0, 0.0},
                        {0.6, 0.4},
                        {0.8, 0.2},
                        {0.2, 0.8}};
 
   vector ap=y_true_bin.ClassificationScore(y_scores_bin,CLASSIFICATION_AVERAGE_PRECISION,AVERAGE_BINARY);
   Print("average precision score binary = ",ap);
   vector ap2=y_true_bin.ClassificationScore(y_score1_bin,CLASSIFICATION_AVERAGE_PRECISION,AVERAGE_BINARY);
   Print("average precision score binary = ",ap2);
   vector ap3=y_true_bin.ClassificationScore(y_scores_bin,CLASSIFICATION_AVERAGE_PRECISION,AVERAGE_NONE);
   Print("average precision score none = ",ap3);
   Print("");
 
   vector area=y_true_bin.ClassificationScore(y_scores_bin,CLASSIFICATION_ROC_AUC,AVERAGE_BINARY);
   Print("roc auc score binary = ",area);
   vector area2=y_true_bin.ClassificationScore(y_score1_bin,CLASSIFICATION_ROC_AUC,AVERAGE_BINARY);
   Print("roc auc score binary = ",area2);
   vector area3=y_true_bin.ClassificationScore(y_scores_bin,CLASSIFICATION_ROC_AUC,AVERAGE_NONE);
   Print("roc auc score none = ",area3);
 
 
/*
  top 1 accuracy score = [0.6666666666666666]
  top 2 accuracy score = [1]
  top k = [0.75]
  
  average precision score micro = [0.8513333333333333]
  average precision score macro = [0.9326666666666666]
  average precision score weighted = [0.9333333333333333]
  average precision score none = [1,1,0.7,1,0.9266666666666666,0.8333333333333333,1,0.8666666666666667,1,1]
  
  roc auc score micro = [0.9839506172839506]
  roc auc score macro = [0.9892068783068803]
  roc auc score weighted = [0.9887354497354497]
  roc auc score none = [1,1,0.9506172839506173,1,0.984,0.9821428571428571,1,0.9753086419753086,1,1]
  
  average precision score binary = [0.7961904761904761]
  average precision score binary = [0.7961904761904761]
  average precision score none = [0.7678571428571428,0.7961904761904761]
  
  roc auc score binary = [0.7]
  roc auc score binary = [0.7]
  roc auc score none = [0.7,0.7]
*/

7.10.10 PrecisionRecall

计算值以构建精确调用曲线。与ClassificationScore类似，此方法应用于真值向量。

bool vector::PrecisionRecall( const matrix& pred_scores, // 包含每类概率分布的矩阵 const ENUM_ENUM_AVERAGE_MODE mode // 平均模式 matrix& precision, // 计算每个阈值的精确值 matrix& recall, // 计算每个阈值的调用值 matrix& thresholds, // 以降序排列阈值 );

参数

pred_scores

[in] 包含一组水平向量（含有每个类的概率）的矩阵。矩阵行数必须与真值向量的大小相对应。

模式

[in] ENUM_AVERAGE_MODE枚举的平均模式。只使用AVERAGE_NONE，AVERAGE_BINARY和AVERAGE_MICRO。

precision

[out] 包含计算精度曲线值的矩阵。如果不使用平均模式 (AVERAGE_NONE)，则矩阵中的行数对应于模型类的数量。列数对应于真值向量的大小（或概率分布矩阵pred_score中的行数）。在微平均的情况下，矩阵中的行数对应于阈值的总数，不包括重复项。

recall

[out] 包含计算调用曲线值的矩阵。

threshold

[out] 对概率矩阵进行排序得到的阈值矩阵

注意

请参阅ClassificationScore方法的注释。

例如

从mnist.onnx模型收集统计数据的示例（99%准确率）。

//--- 分类指标数据 vectorf y_true(images); vectorf y_pred(images); matrixf y_scores(images,10);

//--- 输入输出 matrixf image(28,28); vectorf result(10);

//--- 测试 for(int test=0; test<images; test++) { image=test_data[test].image; if(!OnnxRun(model,ONNX_DEFAULT,image,result)) { Print("OnnxRun error ",GetLastError()); break; } result.Activation(result,AF_SOFTMAX);

 //--- 收集数据
  y_true[test]=(float)test_data[test].label;
  y_pred[test]=(float)result.ArgMax();
  y_scores.Row(result,test);
 }    }

Accuracy calculation

vectorf accuracy=y_pred.ClassificationMetric(y_true,CLASSIFICATION_ACCURACY); PrintFormat("accuracy=%f",accuracy[0]);

accuracy=0.989000

绘制精确调用图的示例，其中精确值绘制在y轴上，调用值绘制在x轴上。此外，精度图和调用图也分别绘制，阈值绘制在x轴上

    if(y_true.PrecisionRecall(y_scores,AVERAGE_MICRO,mat_precision,mat_recall,mat_thres))
     {
      double precision[],recall[],thres[];
      ArrayResize(precision,mat_thres.Cols());
      ArrayResize(recall,mat_thres.Cols());
      ArrayResize(thres,mat_thres.Cols());
 
      for(uint i=0; i<thres.Size(); i++)
        {
         precision[i]=mat_precision[0][i];
         recall[i]=mat_recall[0][i];
         thres[i]=mat_thres[0][i];
        }
      thres[0]=thres[1]+0.001;
 
      PlotCurve("Precision-Recall curve (micro average)","p-r","",recall,precision);
      Plot2Curves("Precision-Recall (micro average)","precision","recall",thres,precision,recall);
     }

Resulting curves:

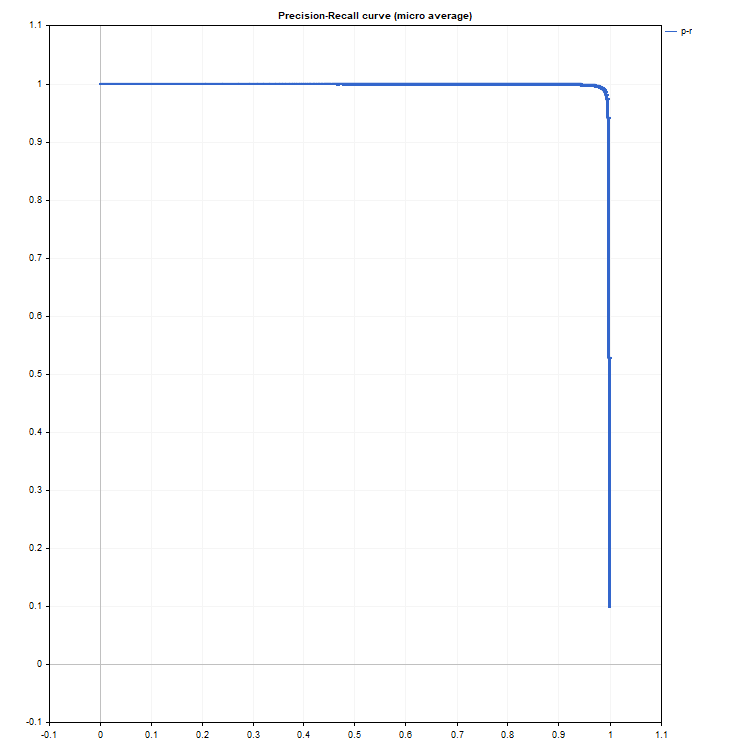
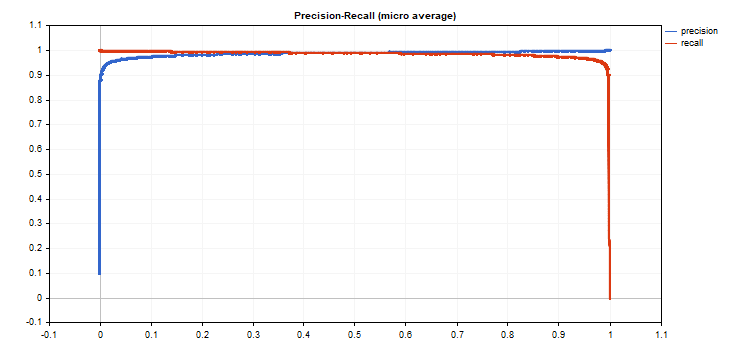
7.10.11 ReceiverOperatingCharacteristic

计算值以构建接收器工作特性(ROC)曲线。与ClassificationScore类似，此方法应用于真值向量。

bool vector::ReceiverOperatingCharacteristic(
   const matrix&                 pred_scores,   // 包含每类概率分布的矩阵
   const ENUM_ENUM_AVERAGE_MODE  mode           // 平均模式
   matrix&                       fpr,           // 计算每个阈值的假阳性率值
   matrix&                       tpr,           // 计算每个阈值的真阳性率值
   matrix&                       thresholds,    // 以降序排列阈值
   );

参数

pred_scores

[in] 包含一组水平向量（含有每个类的概率）的矩阵。矩阵行数必须与真值向量的大小相对应。

模式

[in] ENUM_AVERAGE_MODE枚举的平均模式。只使用AVERAGE_NONE，AVERAGE_BINARY和AVERAGE_MICRO。

fpr

[out] 假阳性率曲线计算值的矩阵。如果不使用平均模式 (AVERAGE_NONE)，则矩阵中的行数对应于模型类的数量。列数对应于真值向量的大小（或概率分布矩阵pred_score中的行数）。在微平均的情况下，矩阵中的行数对应于阈值的总数，不包括重复项。

tpr

[out] 真阳性率曲线计算值的矩阵。

threshold

[out] 对概率矩阵进行排序得到的阈值矩阵

注意

请参阅ClassificationScore方法的注释。

例如

绘制ROC图的示例，其中tpr值绘制在y轴上，fpr值绘制在x轴上。此外，fpr图和tpr图也分别绘制，阈值绘制在x轴上

   matrixf mat_thres;
   matrixf mat_fpr;
   matrixf mat_tpr;
 
   if(y_true.ReceiverOperatingCharacteristic(y_scores,AVERAGE_MICRO,mat_fpr,mat_tpr,mat_thres))
     {
      double fpr[],tpr[],thres[];
      ArrayResize(fpr,mat_thres.Cols());
      ArrayResize(tpr,mat_thres.Cols());
      ArrayResize(thres,mat_thres.Cols());
 
      for(uint i=0; i<fpr.Size(); i++)
        {
         fpr[i]=mat_fpr[0][i];
         tpr[i]=mat_tpr[0][i];
         thres[i]=mat_thres[0][i];
        }
      thres[0]=thres[1]+0.001;
 
      PlotCurve("ROC curve (micro average)","roc","0.5",fpr,tpr);
      Plot2Curves("fpr-tpr (micro average)","fpr","tpr",thres,fpr,tpr);
     }

结果曲线：

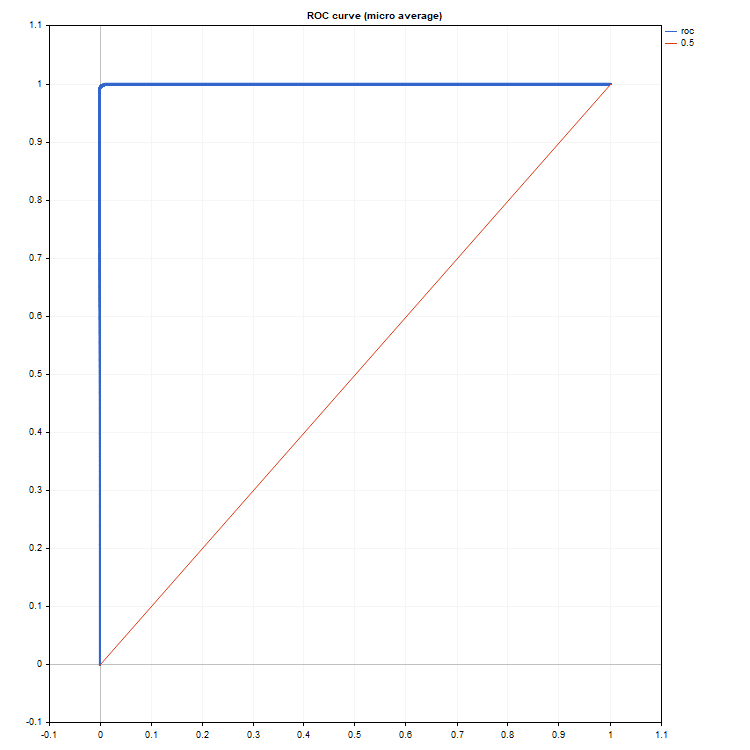
图形输出代码很简单，并且基于<Graphics/Graphic.mqh>标准库。

示例使用mnist.onnx模型的数据。代码在PrecisionRecall方法描述中展示。

ROC AUC接近理想值。

roc auc score micro = [0.99991]